d3 / d3-geo-projection Goto Github PK

View Code? Open in Web Editor NEW

1.1K 68.0 201.0 26.75 MB

Extended geographic projections for d3-geo.

Home Page: https://observablehq.com/collection/@d3/d3-geo-projection

License: Other

JavaScript 100.00%

d3-geo-projection's Introduction

d3-geo-projection

Extended geographic projections for d3-geo. See Command-Line Cartography for an introduction.

Installing

If you use npm, npm install d3-geo-projection. You can also download the latest release on GitHub. For vanilla HTML in modern browsers, import d3-geo-projection from Skypack:

<script type="module">

import {geoAitoff} from "https://cdn.skypack.dev/d3-geo-projection@4";

const projection = geoAitoff();

</script>

For legacy environments, you can load d3-geo-projection’s UMD bundle from an npm-based CDN such as jsDelivr; a d3 global is exported:

<script src="https://cdn.jsdelivr.net/npm/d3-array@3"></script>
<script src="https://cdn.jsdelivr.net/npm/d3-geo@3"></script>
<script src="https://cdn.jsdelivr.net/npm/d3-geo-projection@4"></script>
<script>

const projection = d3.geoAitoff();

</script>

Projections

Note: projections tagged [d3-geo] are exported by d3-geo, not d3-geo-projection. These commonly-used projections are also included in the d3 default bundle.

# d3.geoAiry() · Source, Examples
# d3.geoAiryRaw(beta)

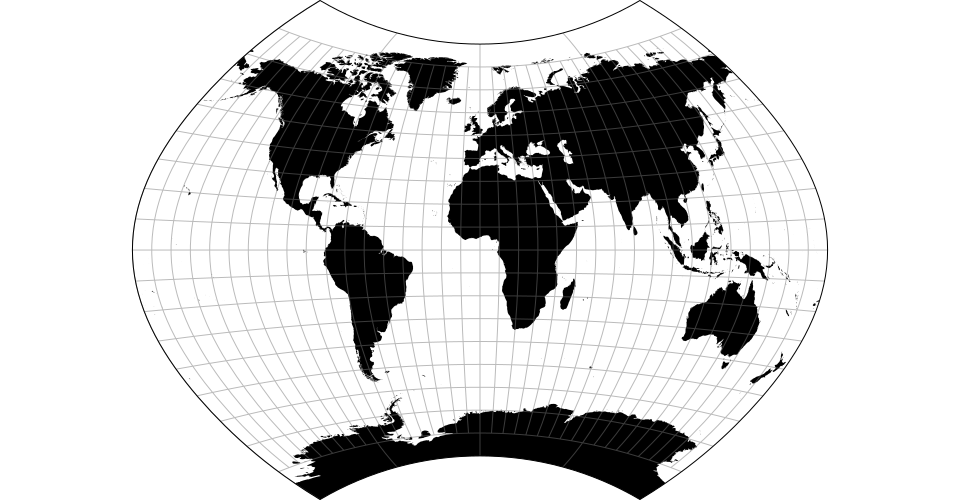
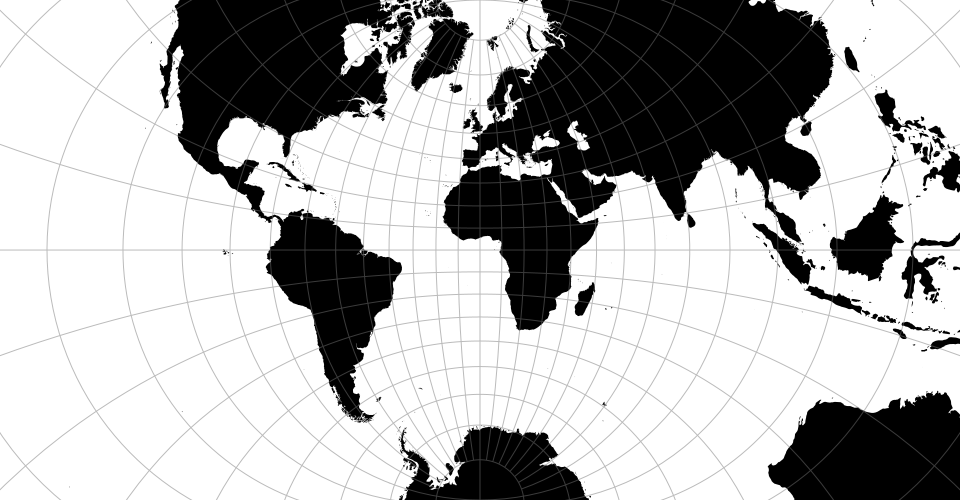
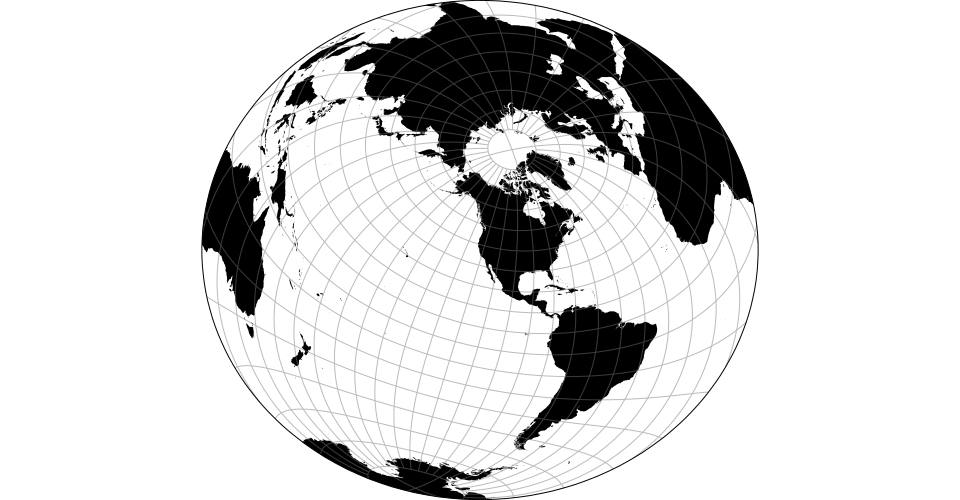
Airy’s minimum-error azimuthal projection.

# airy.radius([radius])

Defaults to 90°.

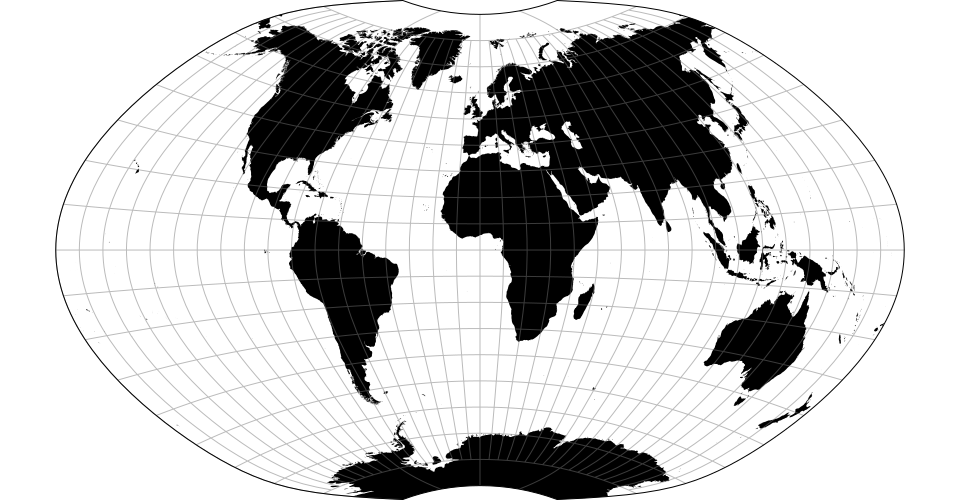
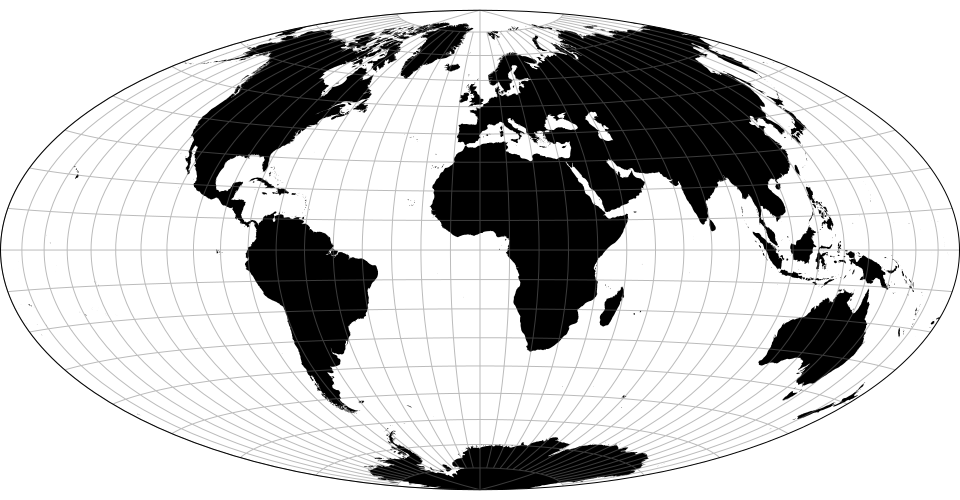
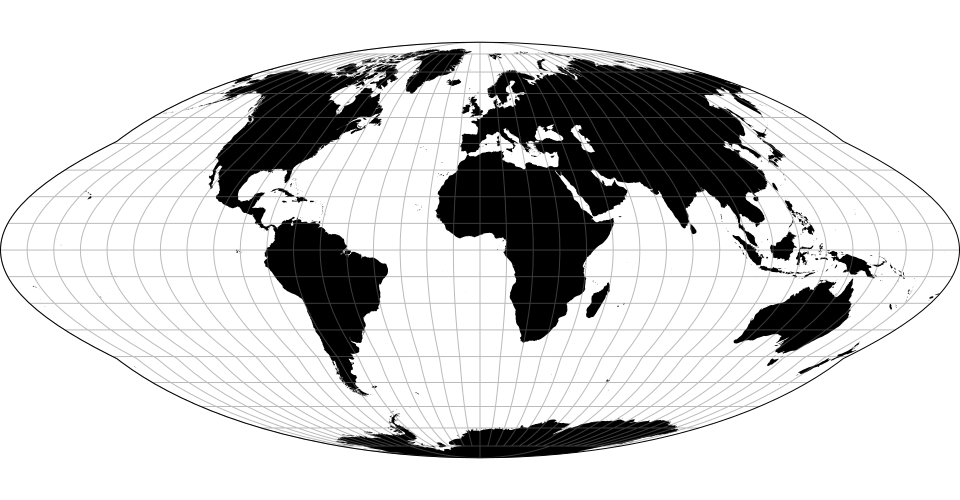
# d3.geoAitoff() · Source, Examples
# d3.geoAitoffRaw

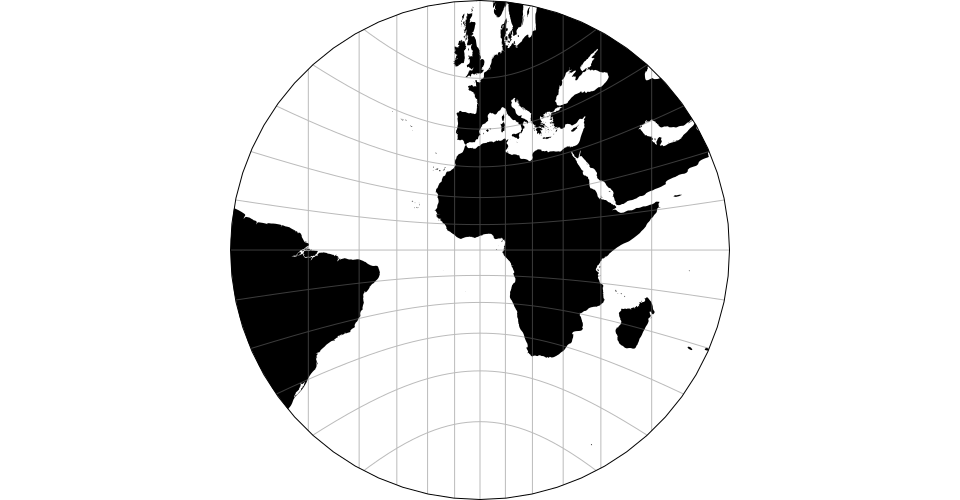
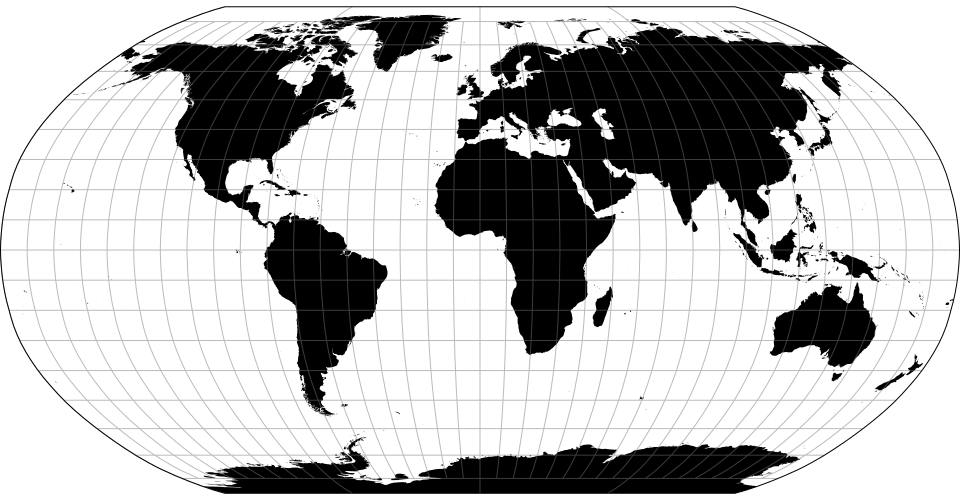
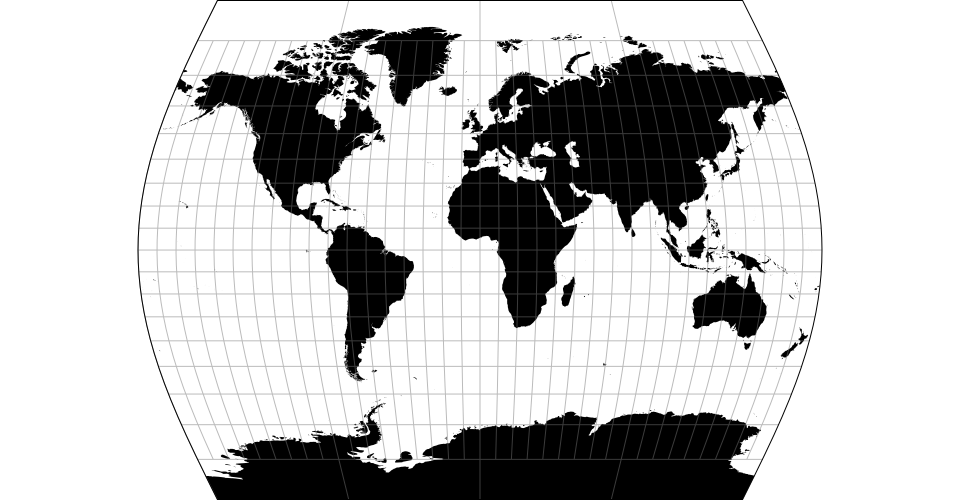
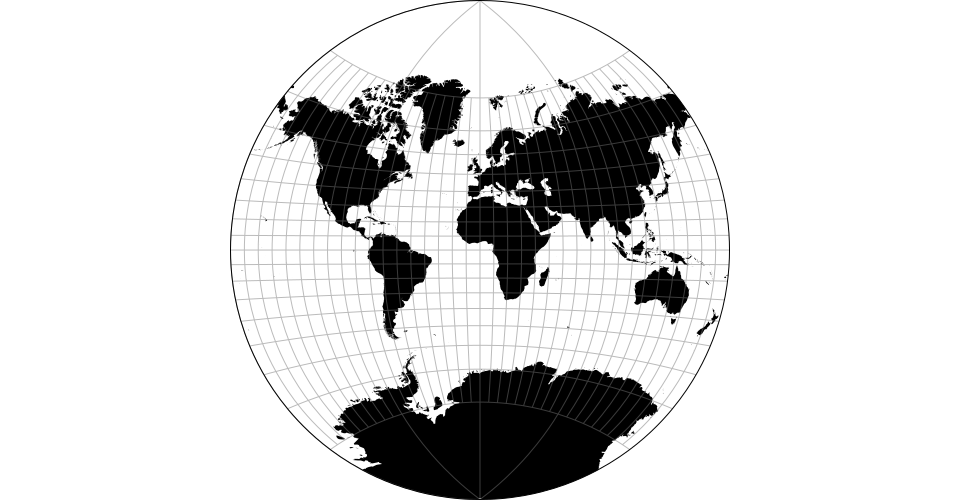
The Aitoff projection.

# d3.geoAlbers() · Source [d3-geo]

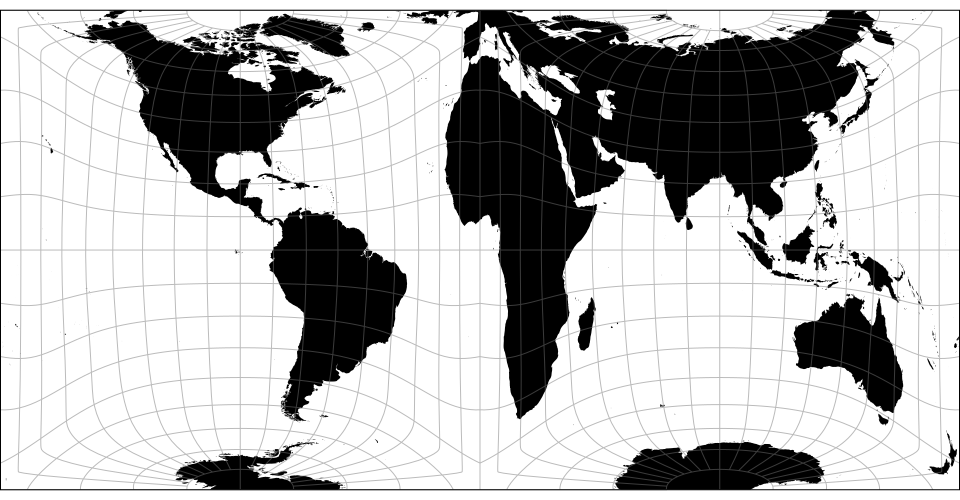
Albers’ equal-area conic projection.

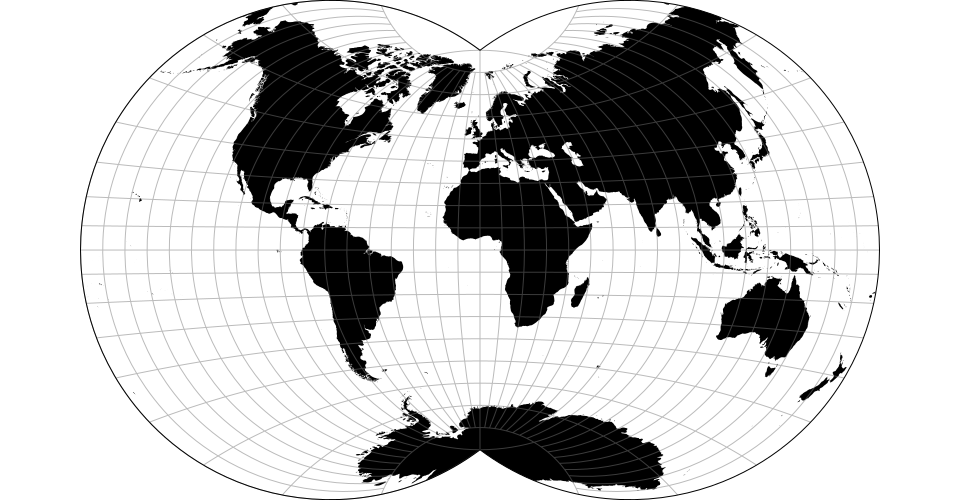
# d3.geoArmadillo() · Source, Examples
# d3.geoArmadilloRaw(phi0)

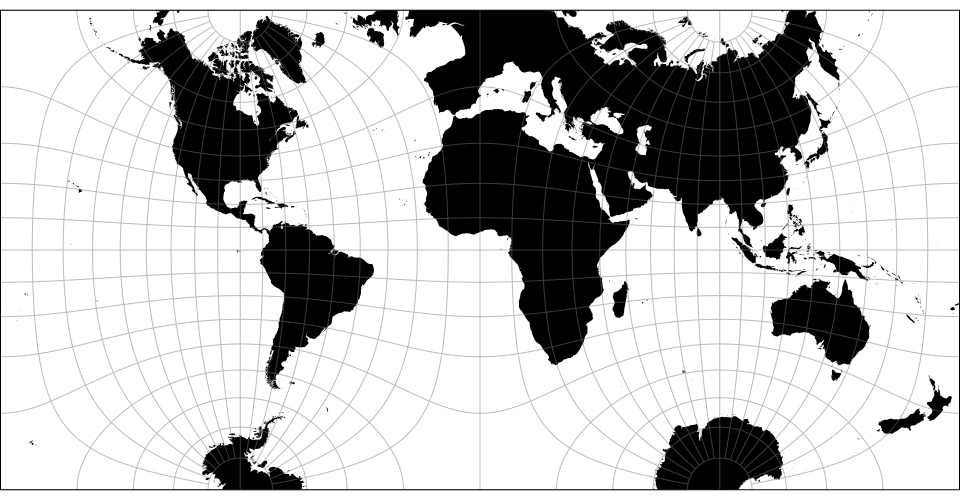
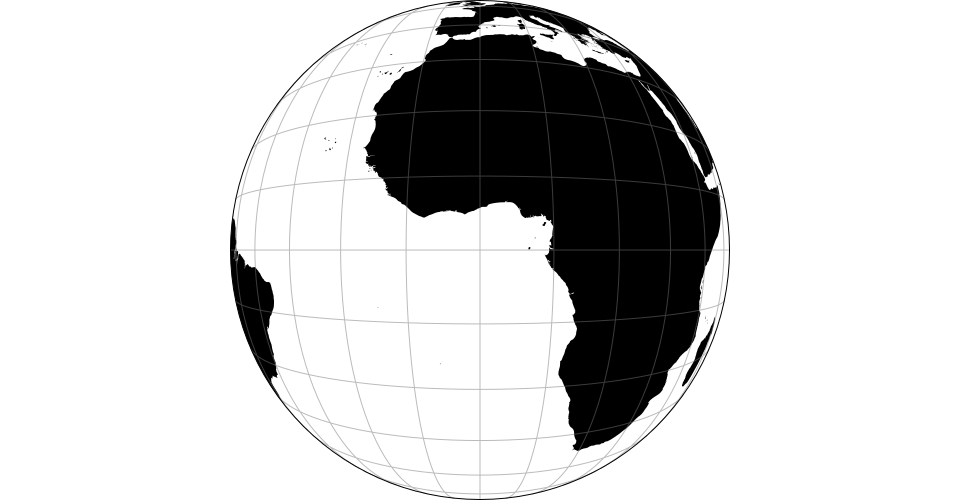
The armadillo projection. The default center assumes the default parallel of 20° and should be changed if a different parallel is used. Note: requires clipping to the sphere.

# armadillo.parallel([parallel])

Defaults to 20°.

# d3.geoAugust() · Source, Examples
# d3.geoAugustRaw

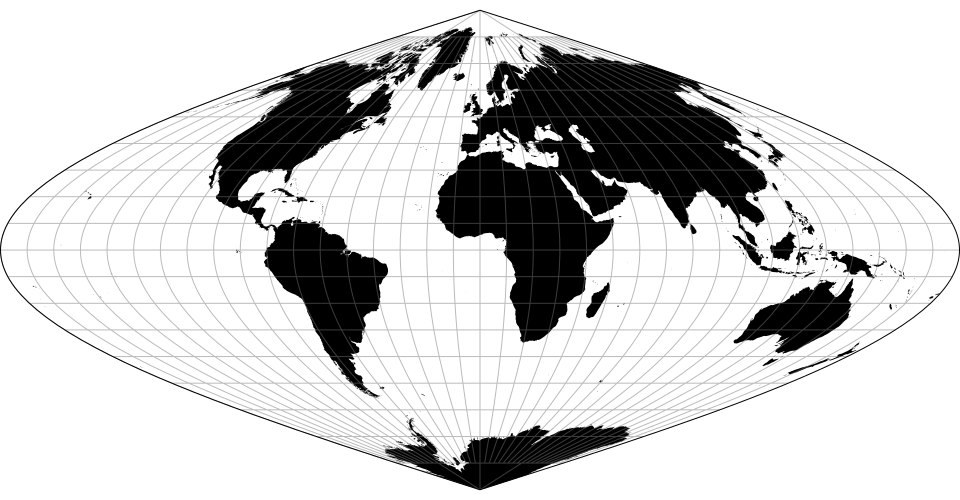
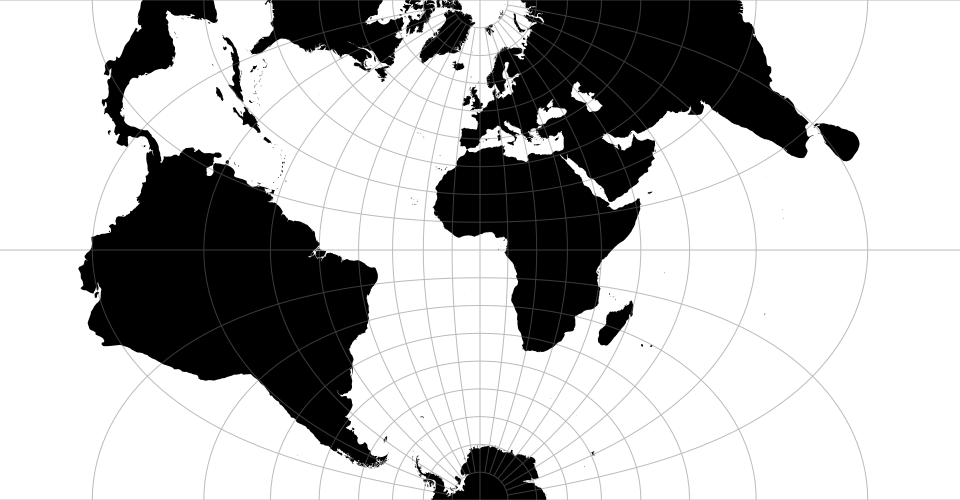
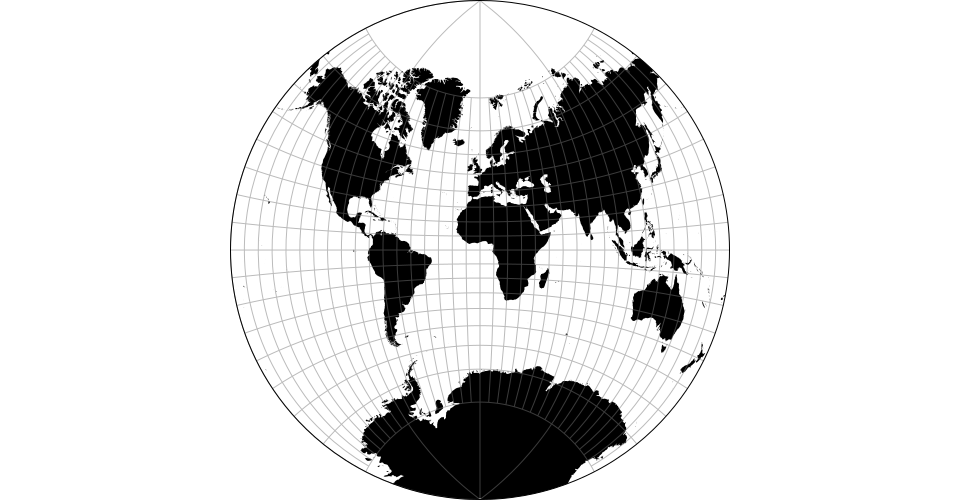
August’s epicycloidal conformal projection.

# d3.geoAzimuthalEqualArea() · Source [d3-geo], Examples
# d3.geoAzimuthalEqualAreaRaw

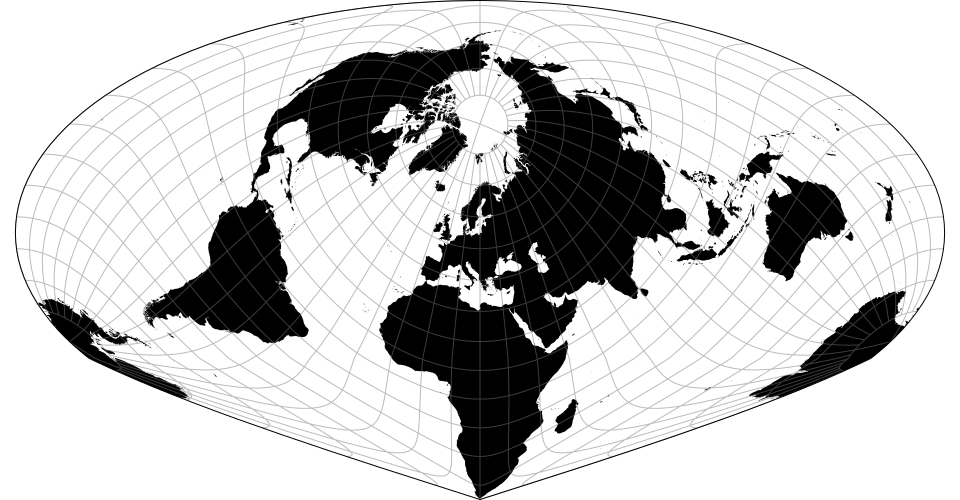
The Lambert azimuthal equal-area projection.

# d3.geoAzimuthalEquidistant() · Source [d3-geo], Examples
# d3.geoAzimuthalEquidistantRaw

The azimuthal equidistant projection.

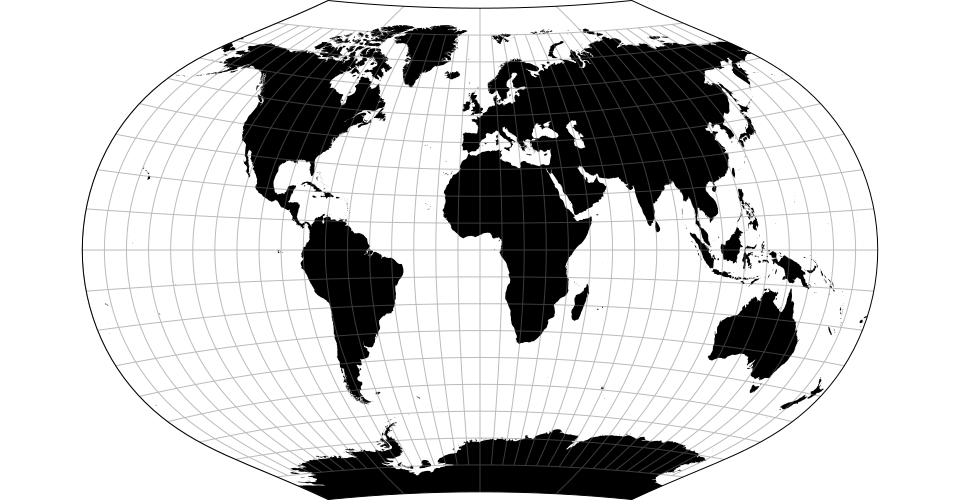
# d3.geoBaker() · Source, Examples
# d3.geoBakerRaw

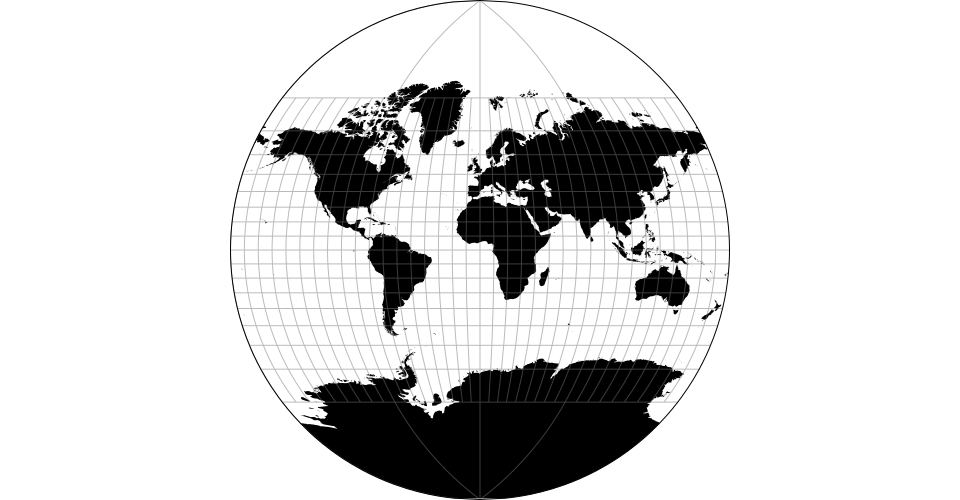
The Baker Dinomic projection.

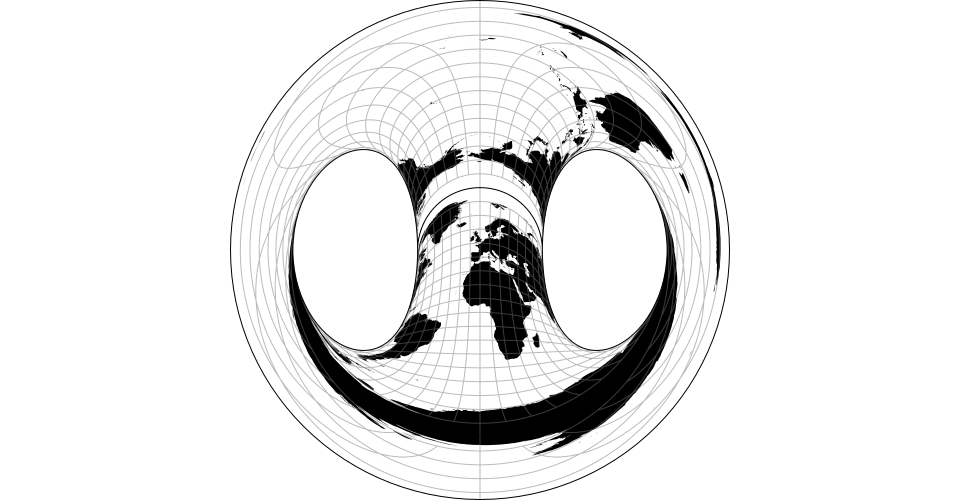
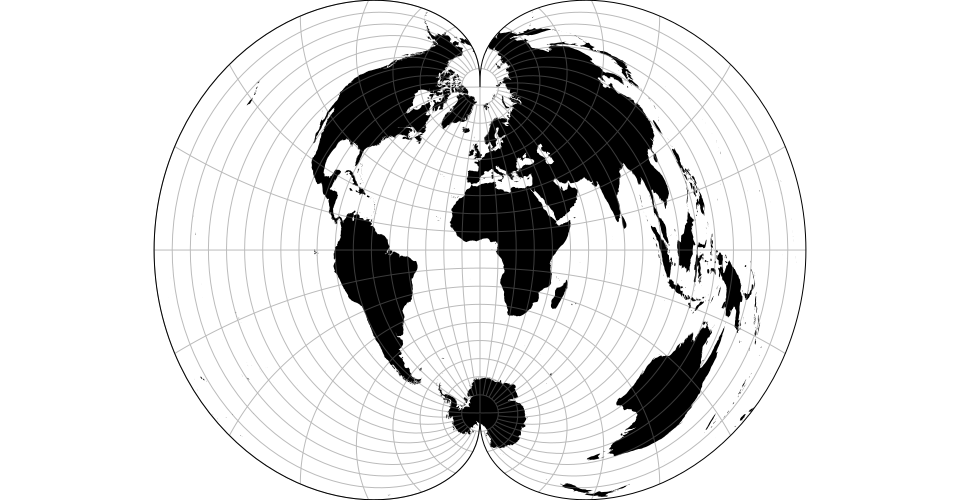
# d3.geoBerghaus() · Source, Examples
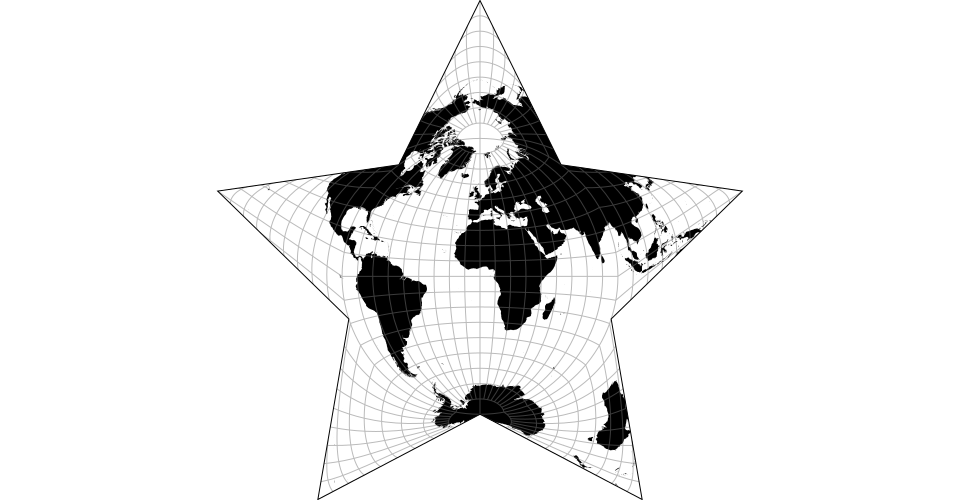
# d3.geoBerghausRaw(lobes)

Berghaus’ star projection. The default center assumes the default lobe number of 5 and should be changed if a different number of lobes is used. Note: requires clipping to the sphere.

# berghaus.lobes([lobes]) · Source

If lobes is specified, sets the number of lobes in the resulting star, and returns this projection. If lobes is not specified, returns the current lobe number, which defaults to 5.

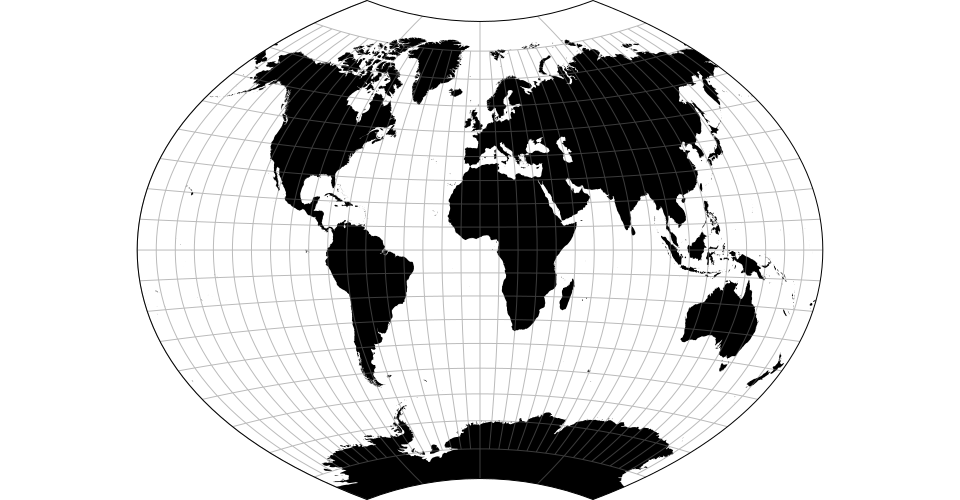
# d3.geoBertin1953() · Source
# d3.geoBertin1953Raw

Jacques Bertin’s 1953 projection.

# d3.geoBoggs() · Source, Examples
# d3.geoBoggsRaw

The Boggs eumorphic projection. More commonly used in interrupted form.

# d3.geoBonne() · Source, Examples
# d3.geoBonneRaw(phi0)

The Bonne pseudoconical equal-area projection. The Werner projection is a limiting form of the Bonne projection with a standard parallel at ±90°. The default center assumes the default parallel of 45° and should be changed if a different parallel is used.

# bonne.parallel([parallel])

Defaults to 45°.

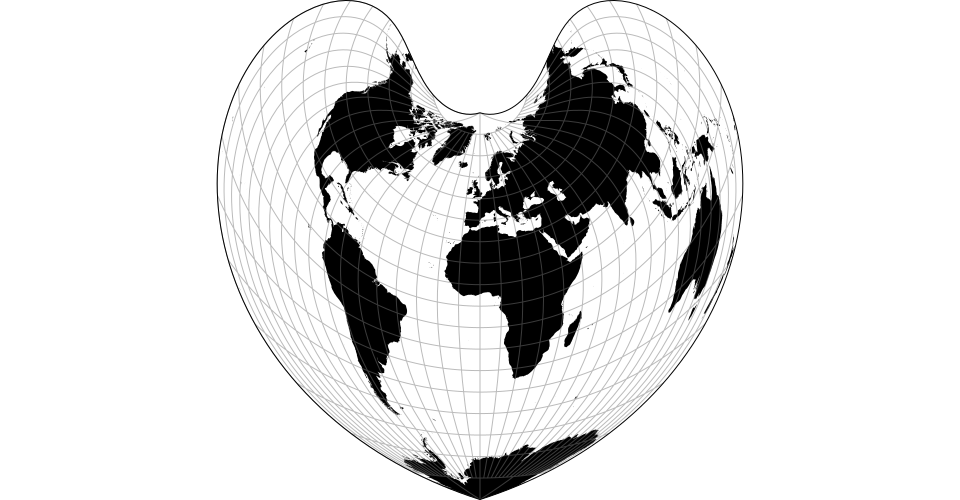
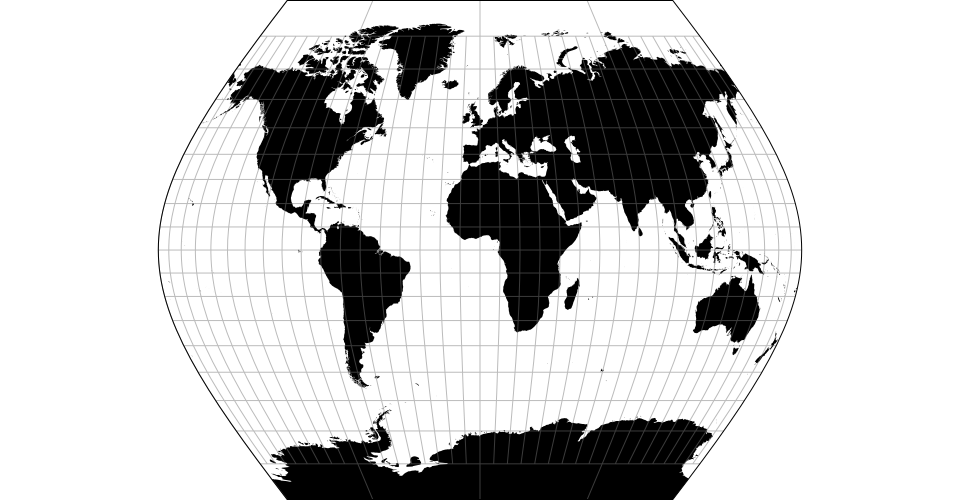
# d3.geoBottomley() · Source, Examples
# d3.geoBottomleyRaw(sinPsi)

The Bottomley projection “draws lines of latitude as concentric circular arcs, with arc lengths equal to their lengths on the globe, and placed symmetrically and equally spaced across the vertical central meridian.”

# bottomley.fraction([fraction])

Defaults to 0.5, corresponding to a sin(ψ) where ψ = π/6.

# d3.geoBromley() · Source, Examples
# d3.geoBromleyRaw

The Bromley projection is a rescaled Mollweide projection.

# d3.geoChamberlin(point0, point1, point2) · Source
# d3.geoChamberlinRaw(p0, p1, p2)

The Chamberlin trimetric projection. This method does not support projection.rotate: the three reference points implicitly determine a fixed rotation.

# d3.geoChamberlinAfrica() · Source

The Chamberlin projection for Africa using points [0°, 22°], [45°, 22°], [22.5°, -22°].

# d3.geoCollignon() · Source, Examples
# d3.geoCollignonRaw

The Collignon equal-area pseudocylindrical projection. This projection is used in the polar areas of the HEALPix projection.

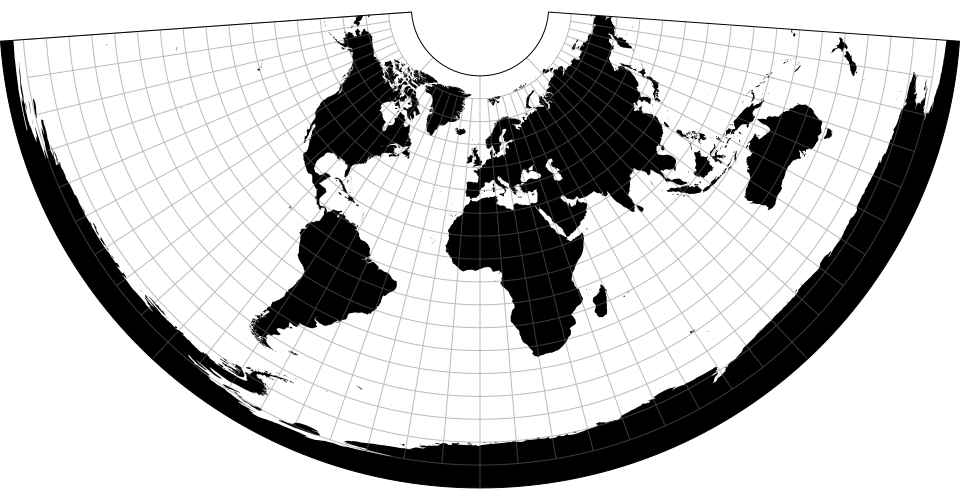
# d3.geoConicConformal() · Source [d3-geo], Examples
# d3.geoConicConformalRaw

The Lambert conformal conic projection.

# d3.geoConicEqualArea() · Source [d3-geo], Examples
# d3.geoConicEqualAreaRaw

Albers’ conic equal-area projection.

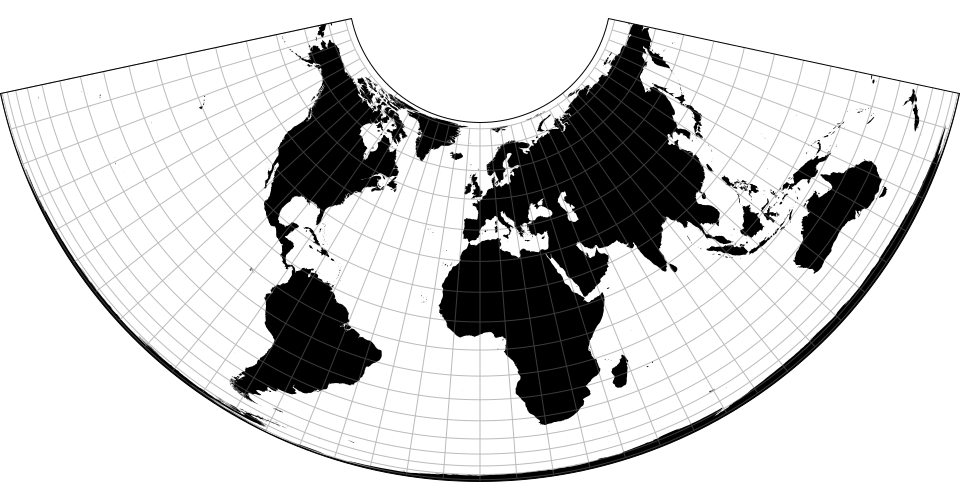
# d3.geoConicEquidistant() · Source [d3-geo], Examples
# d3.geoConicEquidistantRaw

The conic equidistant projection.

# d3.geoCraig() · Source, Examples
# d3.geoCraigRaw(phi)

The Craig retroazimuthal projection. Note: this projection tends to fold over itself if the standard parallel is non-zero; we have not yet implemented the necessary advanced clipping to avoid overlap.

# craig.parallel([parallel])

Defaults to 0°.

# d3.geoCraster() · Source, Examples
# d3.geoCrasterRaw

The Craster parabolic projection; also known as Putniņš P4.

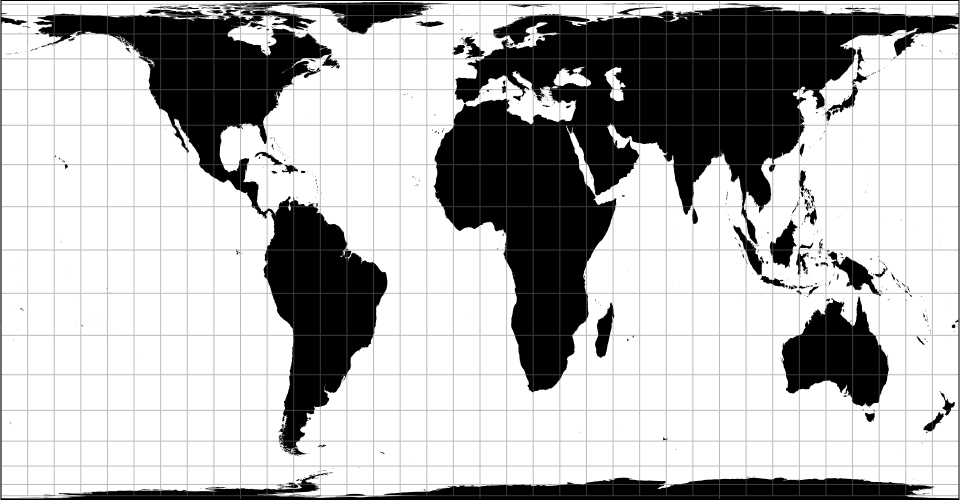
# d3.geoCylindricalEqualArea() · Source, Examples
# d3.geoCylindricalEqualAreaRaw(phi0)

The cylindrical equal-area projection. Depending on the chosen parallel, this projection is also known as the Lambert cylindrical equal-area (0°), Behrmann (30°), Hobo–Dyer (37.5°), Gall–Peters (45°), Balthasart (50°) and Tobler world-in-a-square (~55.654°).

# cylindricalEqualArea.parallel([parallel])

Defaults to approximately 38.58°, fitting the world in a 960×500 rectangle.

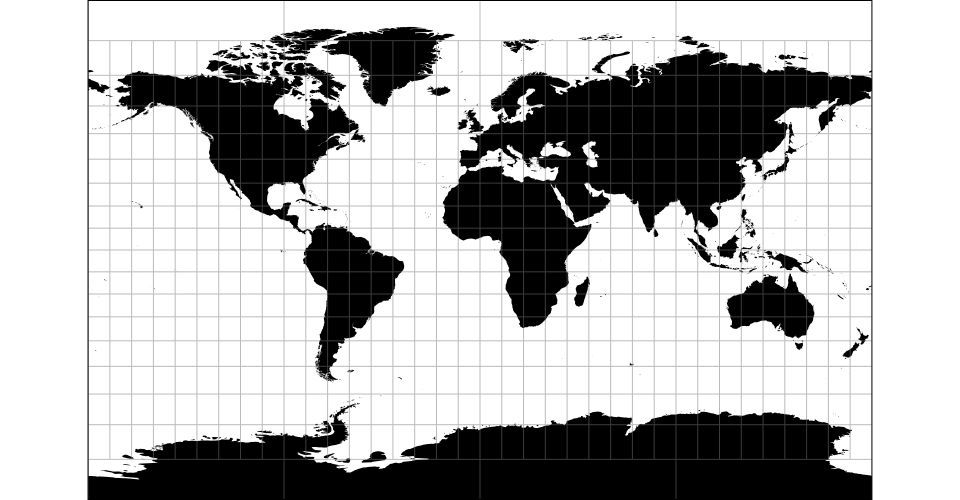
# d3.geoCylindricalStereographic() · Source, Examples
# d3.geoCylindricalStereographicRaw(phi0)

The cylindrical stereographic projection. Depending on the chosen parallel, this projection is also known as Braun’s stereographic (0°) and Gall’s stereographic (45°).

# cylindricalStereographic.parallel([parallel])

Defaults to 0°.

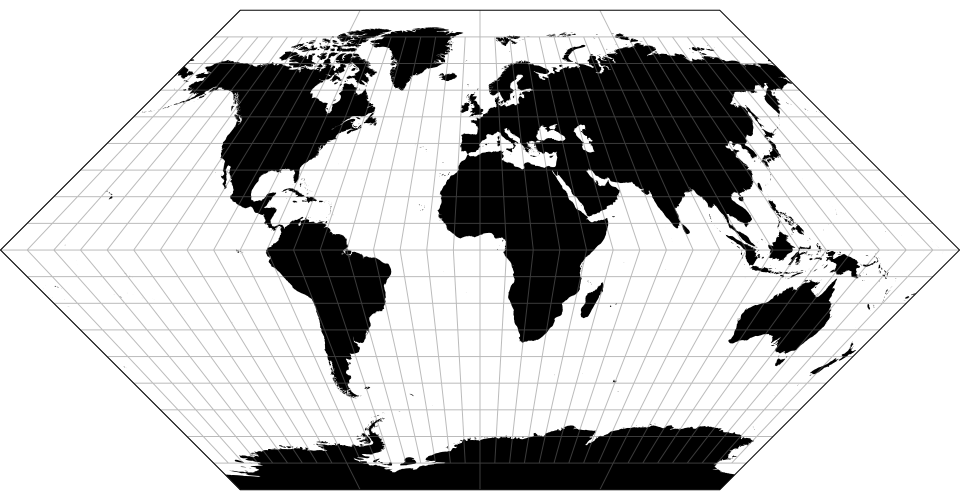
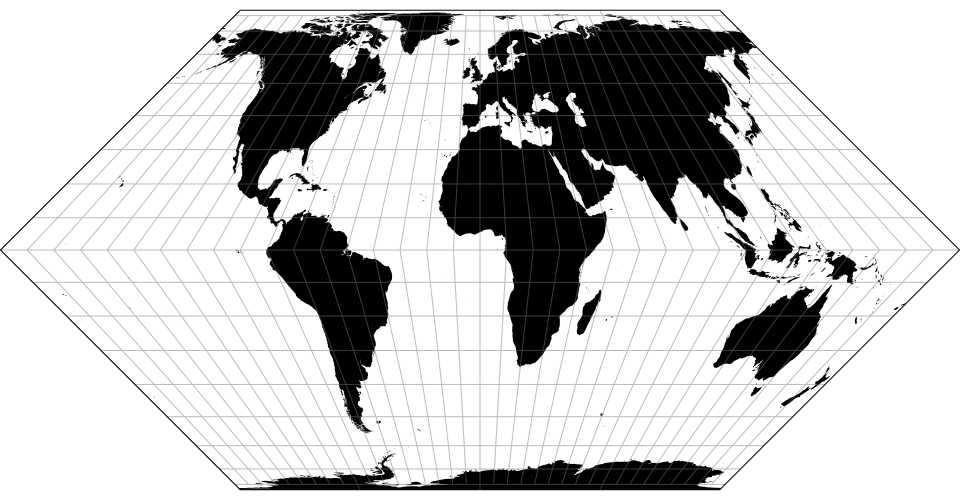
# d3.geoEckert1() · Source, Examples
# d3.geoEckert1Raw

The Eckert I projection.

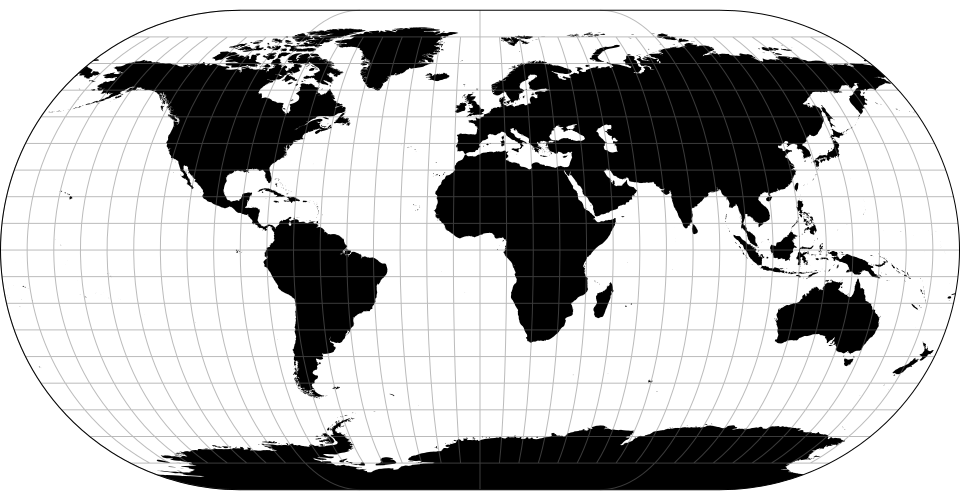
# d3.geoEckert2() · Source, Examples
# d3.geoEckert2Raw

The Eckert II projection.

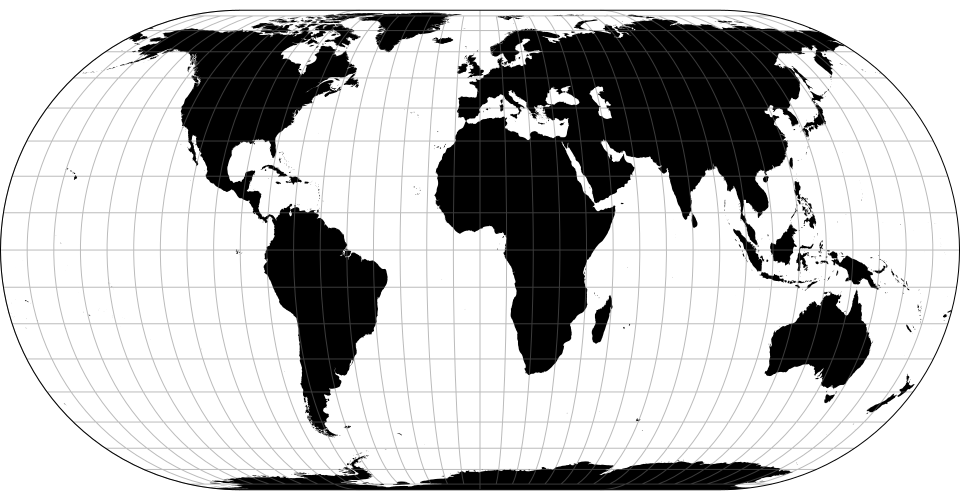
# d3.geoEckert3() · Source, Examples
# d3.geoEckert3Raw

The Eckert III projection.

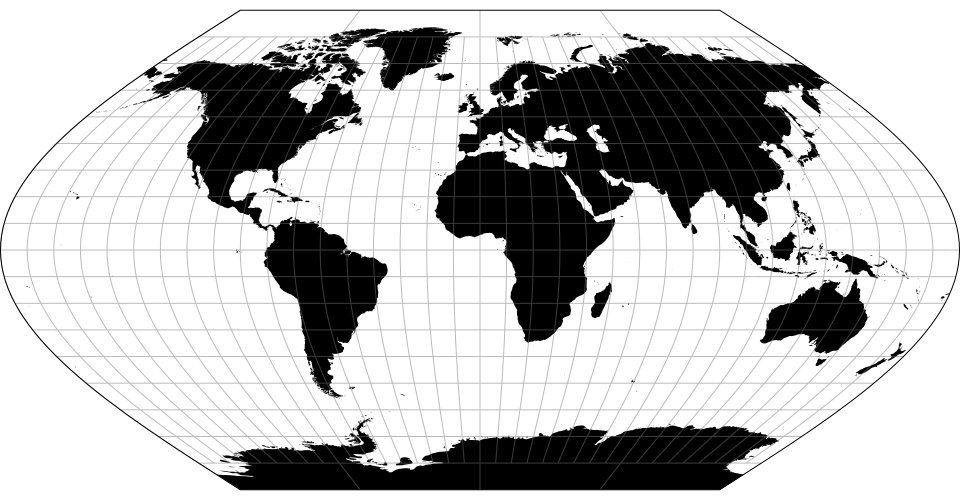
# d3.geoEckert4() · Source, Examples
# d3.geoEckert4Raw

The Eckert IV projection.

# d3.geoEckert5() · Source, Examples
# d3.geoEckert5Raw

The Eckert V projection.

# d3.geoEckert6() · Source, Examples
# d3.geoEckert6Raw

The Eckert VI projection.

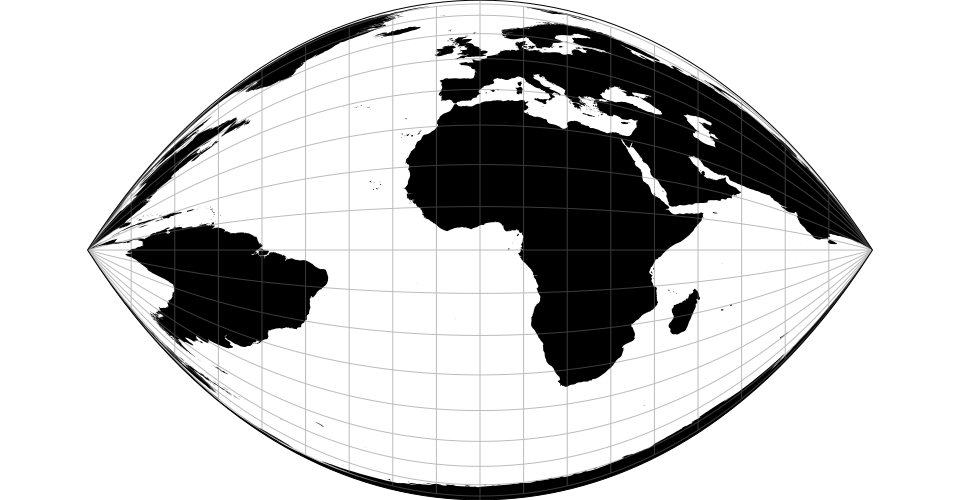
# d3.geoEisenlohr() · Source, Examples
# d3.geoEisenlohrRaw(lambda, phi)

The Eisenlohr conformal projection.

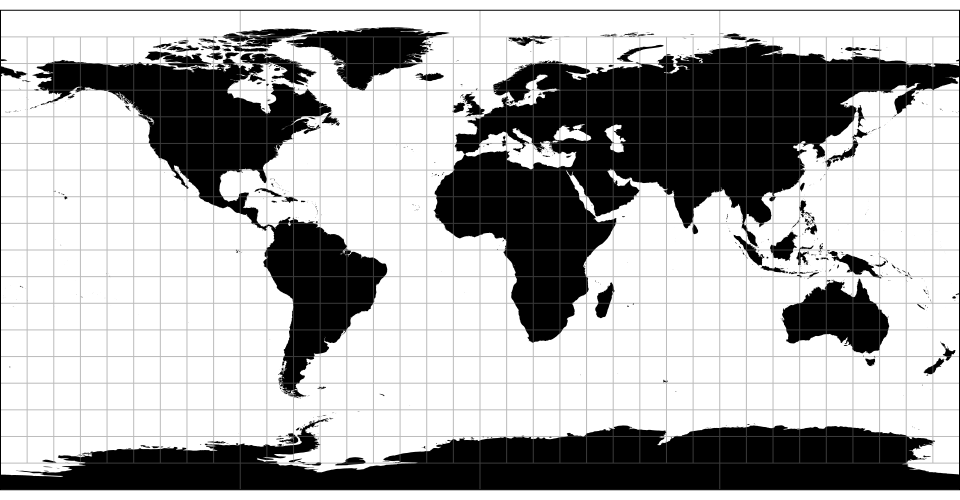
# d3.geoEquirectangular() · Source [d3-geo], Examples
# d3.geoEquirectangularRaw

The equirectangular (plate carrée) projection. The Cassini projection is the transverse aspect of the equirectangular projection.

# d3.geoFahey() · Source, Examples
# d3.geoFaheyRaw

The Fahey pseudocylindrical projection.

# d3.geoFoucaut() · Source, Examples
# d3.geoFoucautRaw

Foucaut’s stereographic equivalent projection.

# d3.geoFoucautSinusoidal() · Source, Examples
# d3.geoFoucautSinusoidalRaw

Foucaut’s sinusoidal projection, an equal-area average of the sinusoidal and Lambert’s cylindrical projections.

# foucautSinusoidal.alpha([alpha])

Relative weight of the cylindrical projection. Defaults to 0.5.

# d3.geoGilbert([type]) · Source, Examples

Gilbert’s two-world perspective projection. Wraps an instance of the specified projection type; if not specified, defaults to d3.geoOrthographic.

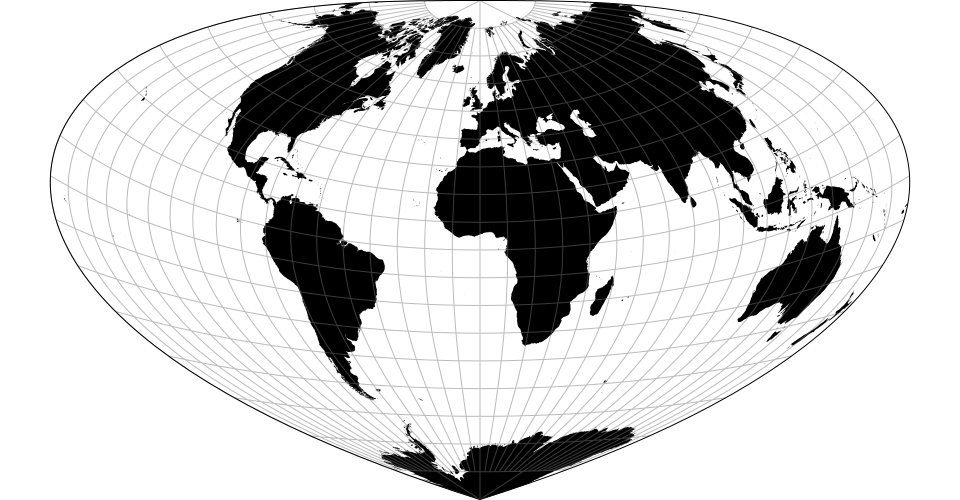
# d3.geoGingery() · Source, Examples
# d3.geoGingeryRaw(rho, lobes)

The U.S.-centric Gingery world projection, as inspired by Cram’s Air Age. Note: requires clipping to the sphere.

# gingery.radius([radius]) · Source

Defaults to 30°.

# gingery.lobes([lobes]) · Source

Defaults to 6.

# d3.geoGinzburg4() · Source, Examples
# d3.geoGinzburg4Raw

The Ginzburg IV projection.

# d3.geoGinzburg5() · Source, Examples
# d3.geoGinzburg5Raw

The Ginzburg V projection.

# d3.geoGinzburg6() · Source, Examples
# d3.geoGinzburg6Raw

The Ginzburg VI projection.

# d3.geoGinzburg8() · Source, Examples
# d3.geoGinzburg8Raw

The Ginzburg VIII projection.

# d3.geoGinzburg9() · Source, Examples
# d3.geoGinzburg9Raw

The Ginzburg IX projection.

# d3.geoGnomonic() · Source [d3-geo], Examples
# d3.geoGnomonicRaw

The gnomonic projection.

# d3.geoGringorten() · Source, Examples
# d3.geoGringortenRaw

The Gringorten square equal-area projection, rearranged to give each hemisphere an entire square.

# d3.geoGuyou() · Source, Examples
# d3.geoGuyouRaw

The Guyou hemisphere-in-a-square projection. Peirce is credited with its quincuncial form.

# d3.geoHammer() · Source, Examples
# d3.geoHammerRaw(A, B)

The Hammer projection. Depending the chosen coefficient and aspect, also known as Eckert–Greifendorff, quartic authalic, and Briesemeister.

# hammer.coefficient([coefficient]) · Source

Defaults to 2.

# d3.geoHammerRetroazimuthal() · Source, Examples
# d3.geoHammerRetroazimuthalRaw(phi0)

The Hammer retroazimuthal projection. Note: requires clipping to the sphere.

# hammerRetroazimuthal.parallel([parallel])

Defaults to 45°.

# d3.geoHealpix() · Source, Examples
# d3.geoHealpixRaw(lobes)

The HEALPix projection: a Hierarchical Equal Area isoLatitude Pixelisation of a 2-sphere. In this implementation, the parameter K is fixed at 3. Note: requires clipping to the sphere.

# healpix.lobes([lobes])

If lobes is specified, sets the number of lobes (the parameter H in the literature) and returns this projection. If lobes is not specified, returns the current lobe number, which defaults to 4.

# d3.geoHill() · Source, Examples
# d3.geoHillRaw(K)

Hill eucyclic projection is pseudoconic and equal-area.

# hill.ratio([ratio])

Defaults to 1. With a ratio of 0, this projection becomes the Maurer No. 73. As it approaches ∞, the projection converges to the Eckert IV.

# d3.geoHomolosine() · Source, Examples
# d3.geoHomolosineRaw

The pseudocylindrical, equal-area Goode homolosine projection is normally presented in interrupted form.

# d3.geoHufnagel() · Source, Examples
# d3.geoHufnagelRaw

A customizable family of pseudocylindrical equal-area projections by Herbert Hufnagel.

# hufnagel.a([a])

# hufnagel.b([b])

# hufnagel.psiMax([psiMax])

# hufnagel.ratio([ratio])

# d3.geoHyperelliptical() · Source, Examples
# d3.geoHyperellipticalRaw

Waldo R. Tobler’s hyperelliptical is a family of equal-area pseudocylindrical projections. Parameters include k, the exponent of the superellipse (or Lamé curve) that defines the shape of the meridians (default k = 2.5); alpha, which governs the weight of the cylindrical projection that is averaged with the superellipse (default alpha = 0); and gamma, that shapes the aspect ratio (default: gamma = 1.183136).

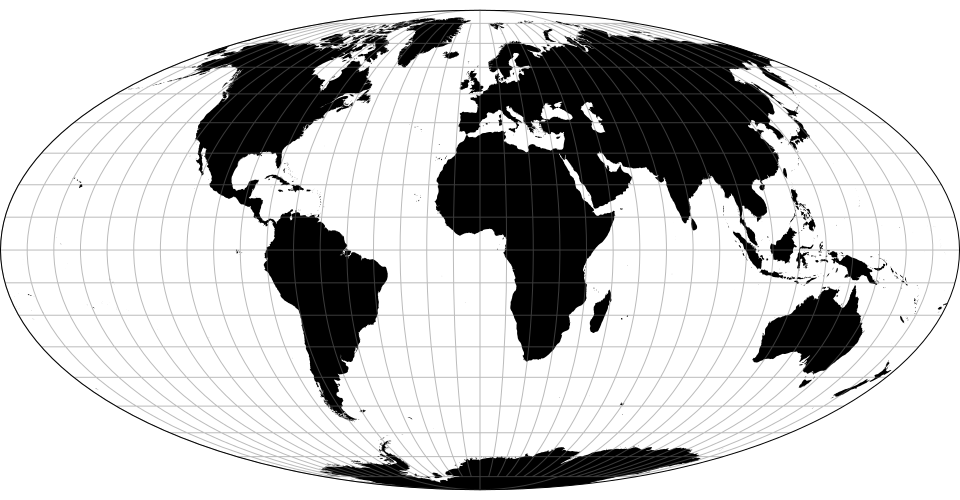
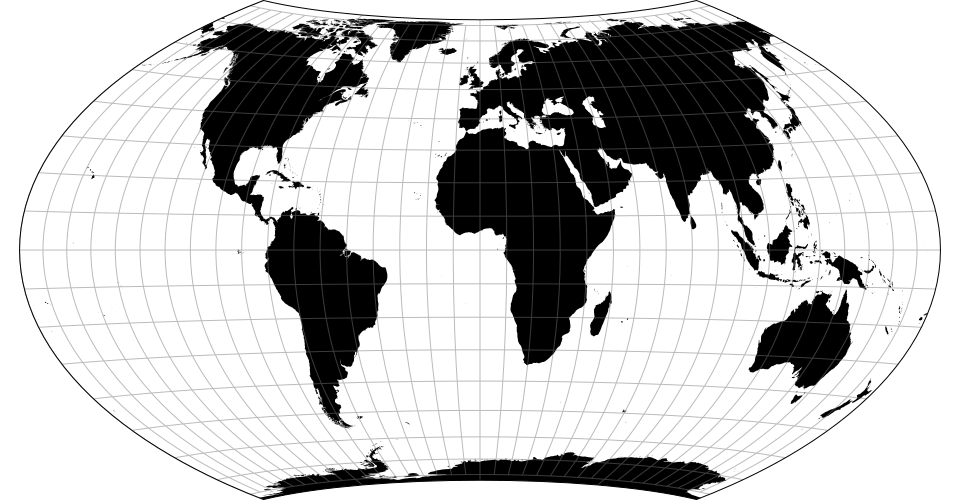
# d3.geoKavrayskiy7() · Source, Examples
# d3.geoKavrayskiy7Raw

The Kavrayskiy VII pseudocylindrical projection.

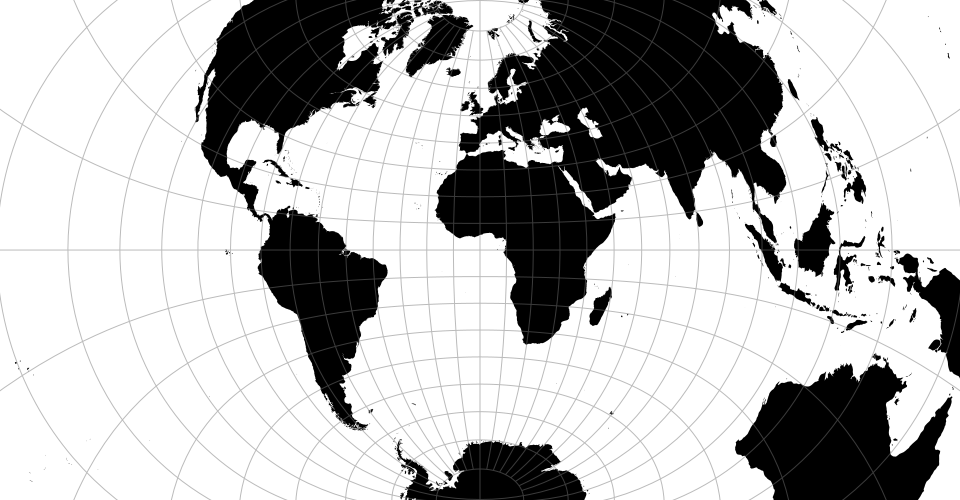
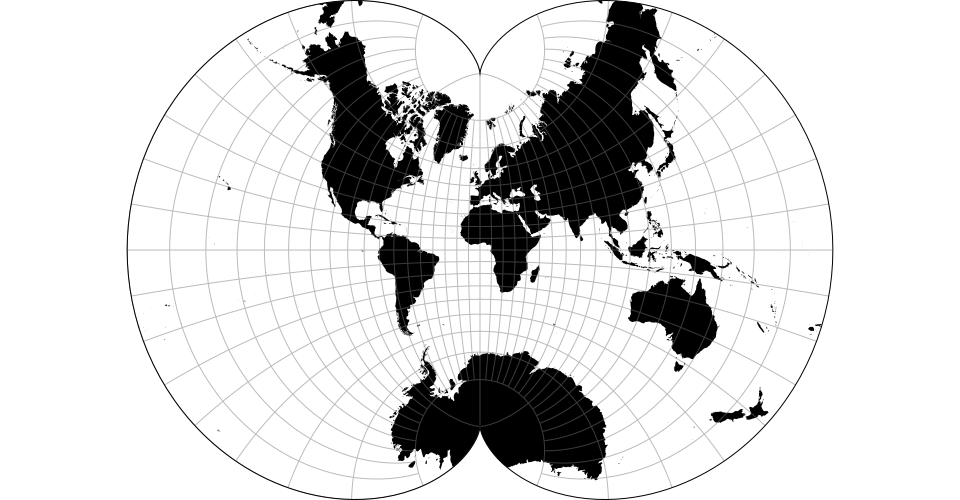
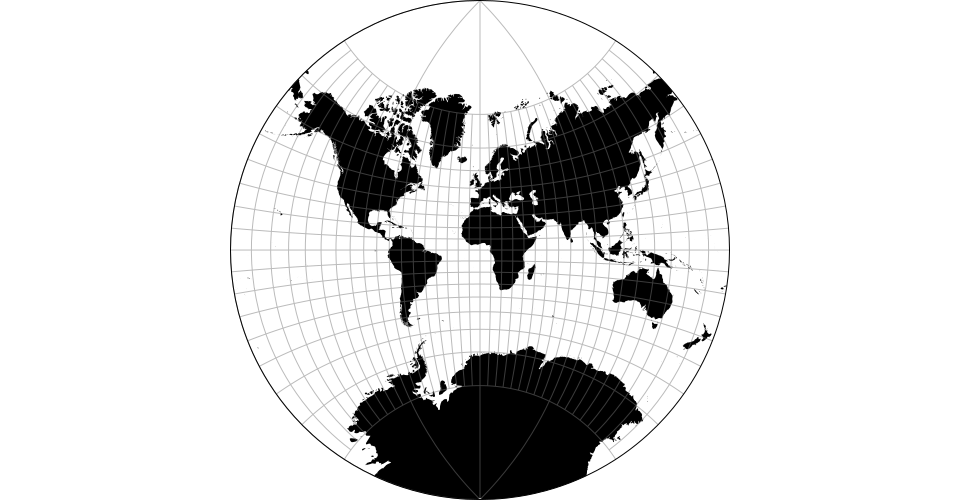
# d3.geoLagrange() · Source, Examples
# d3.geoLagrangeRaw(n)

The Lagrange conformal projection.

# lagrange.spacing([spacing])

Defaults to 0.5.

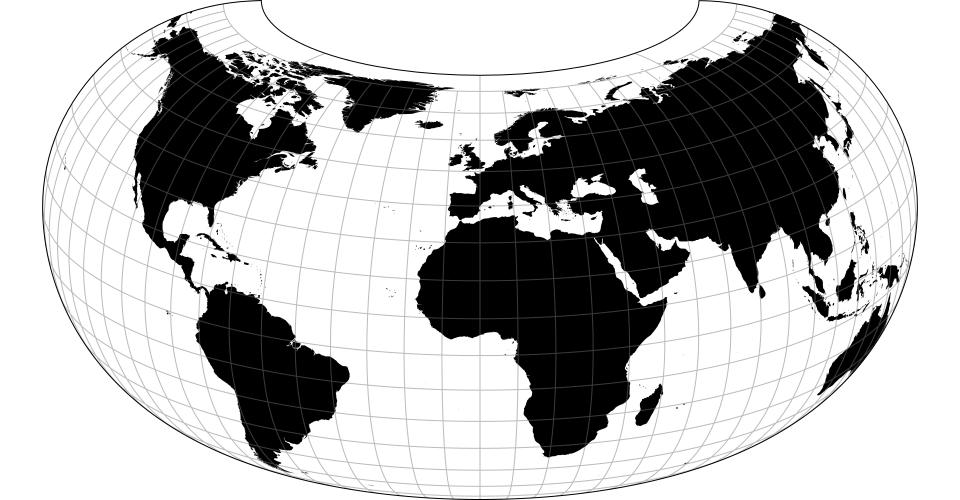
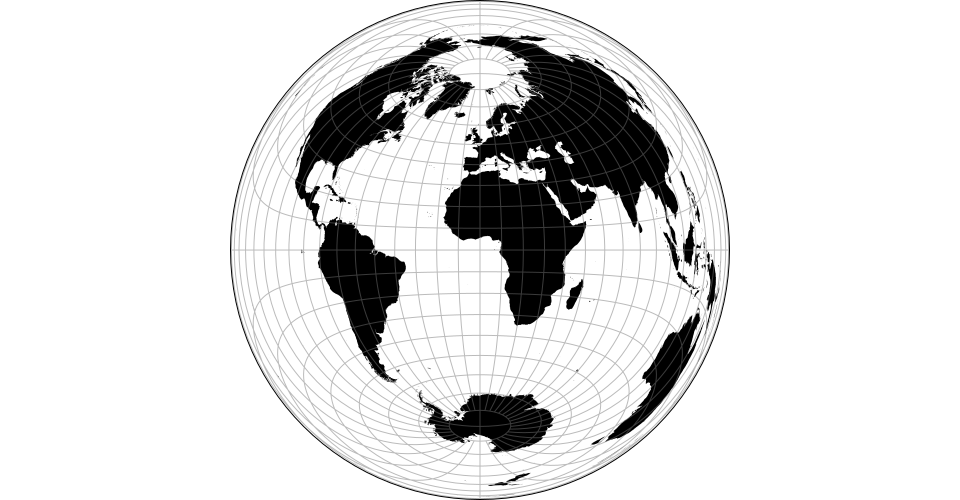
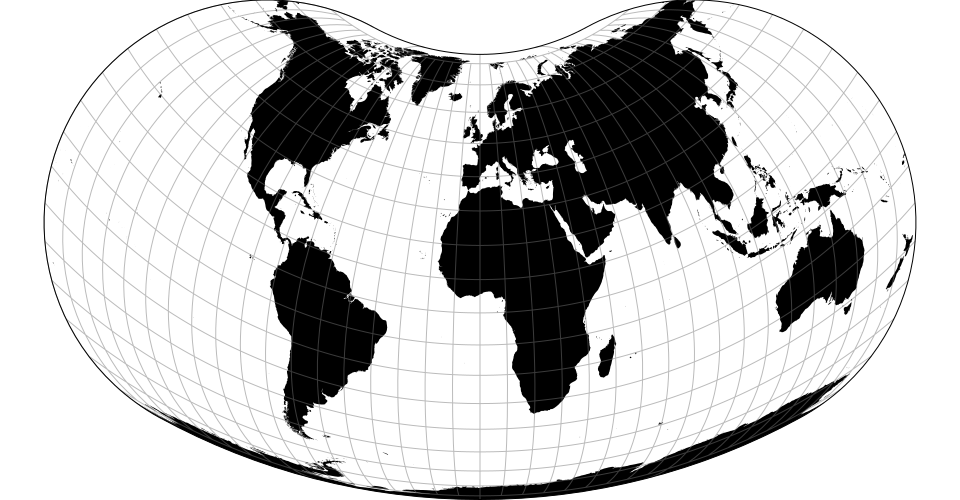
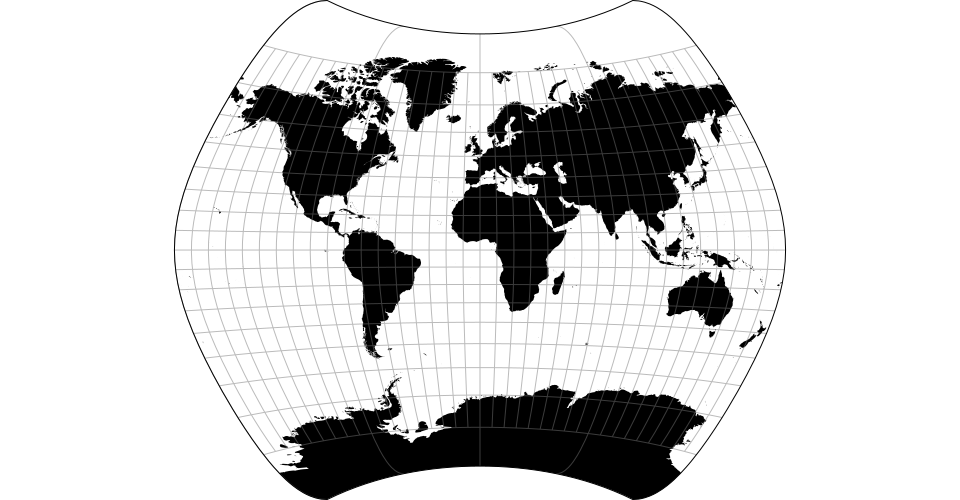
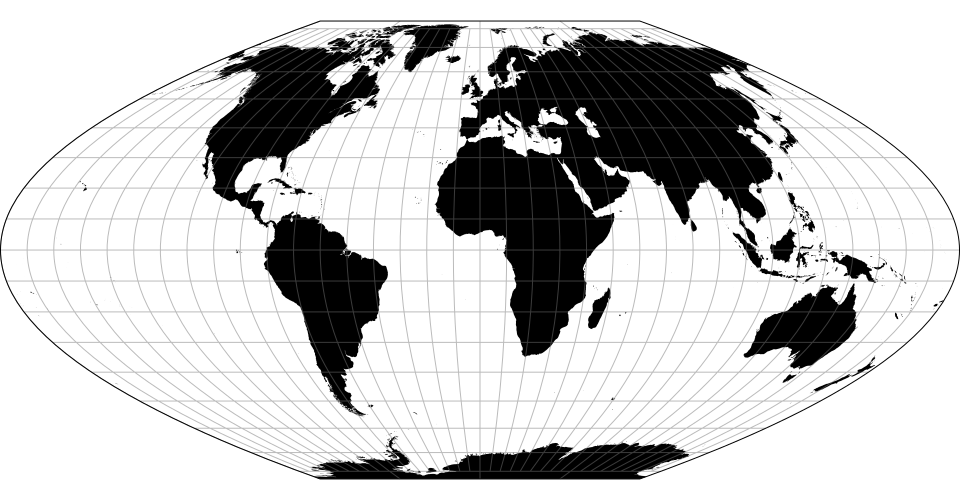
# d3.geoLarrivee() · Source, Examples
# d3.geoLarriveeRaw

The Larrivée projection.

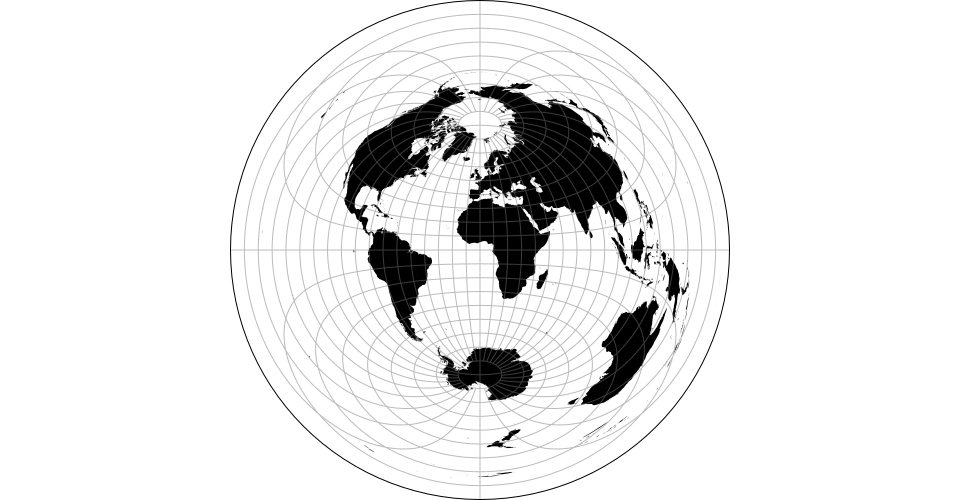
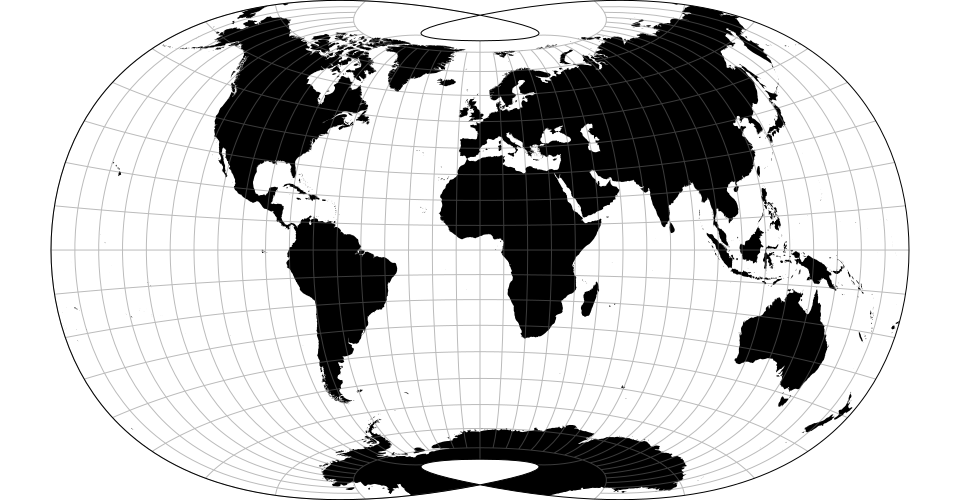
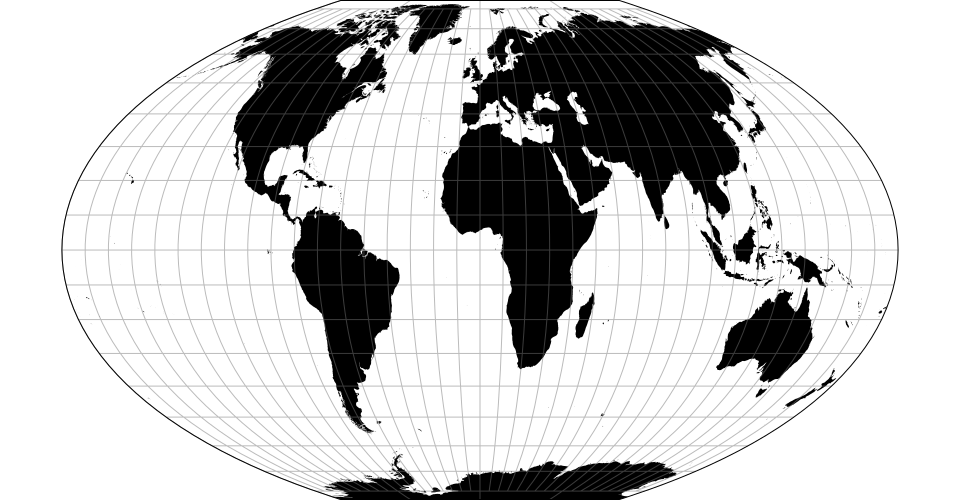
# d3.geoLaskowski() · Source, Examples
# d3.geoLaskowskiRaw

The Laskowski tri-optimal projection simultaneously minimizes distance, angular, and areal distortion.

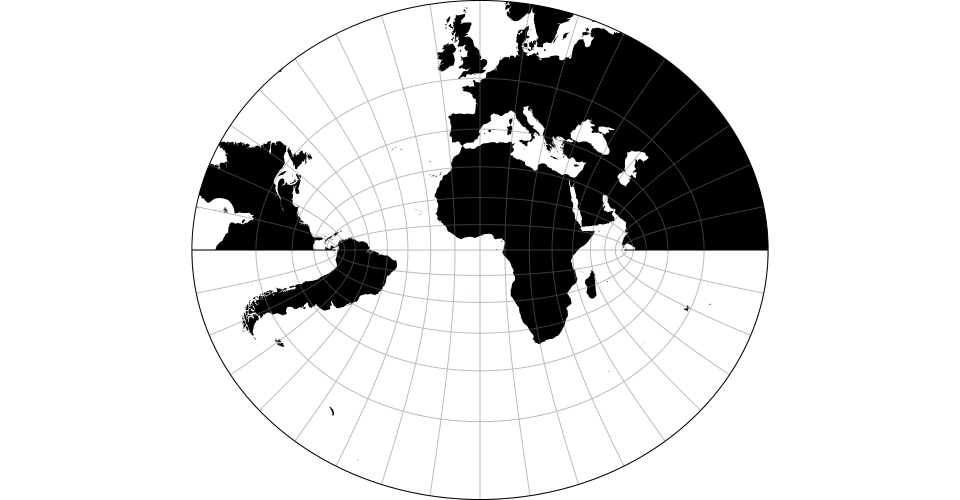
# d3.geoLittrow() · Source, Examples
# d3.geoLittrowRaw

The Littrow projection is the only conformal retroazimuthal map projection. Typically clipped to the geographic extent [[-90°, -60°], [90°, 60°]].

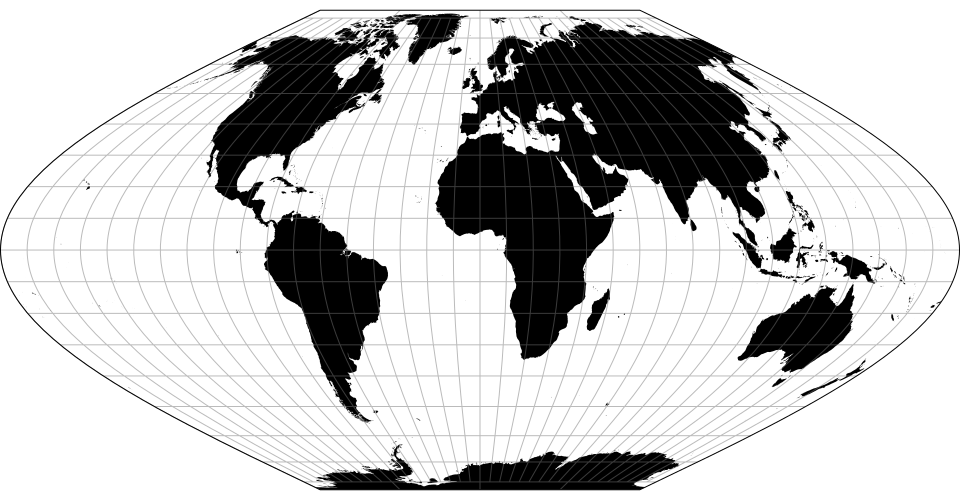
# d3.geoLoximuthal() · Source, Examples
# d3.geoLoximuthalRaw(phi0)

The loximuthal projection is “characterized by the fact that loxodromes (rhumb lines) from one chosen central point (the intersection of the central meridian and central latitude) are shown as straight lines, correct in azimuth from the center, and are ‘true to scale’… It is neither an equal-area projection nor conformal.”

# loximuthal.parallel([parallel])

Defaults to 40°.

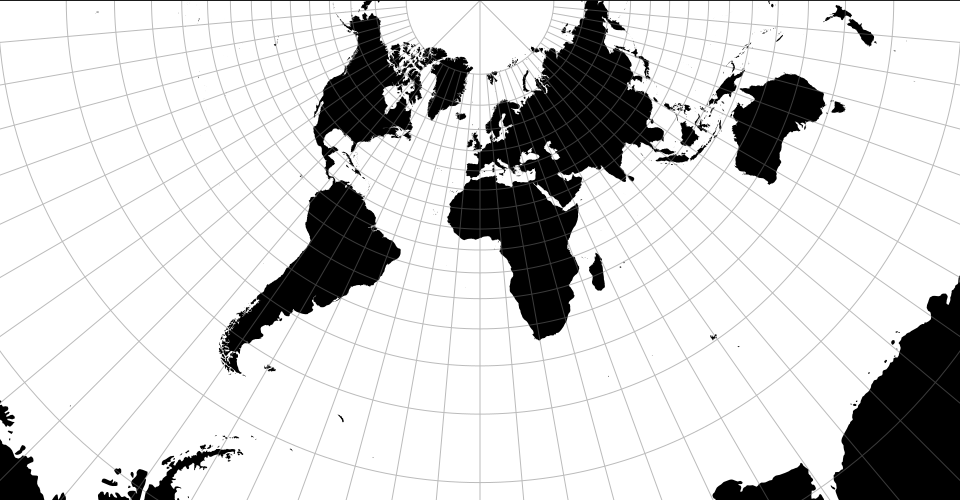
# d3.geoMercator() · Source [d3-geo], Examples
# d3.geoMercatorRaw

The spherical Mercator projection.

# d3.geoMiller() · Source, Examples
# d3.geoMillerRaw

The Miller cylindrical projection is a modified Mercator projection.

# d3.geoModifiedStereographic(coefficients, rotate) · Source
# d3.geoModifiedStereographicRaw(coefficients)

The family of modified stereographic projections. The default clip angle for these projections is 90°. These projections do not support projection.rotate: a fixed rotation is applied that is specific to the given coefficients.

# d3.geoModifiedStereographicAlaska() · Source

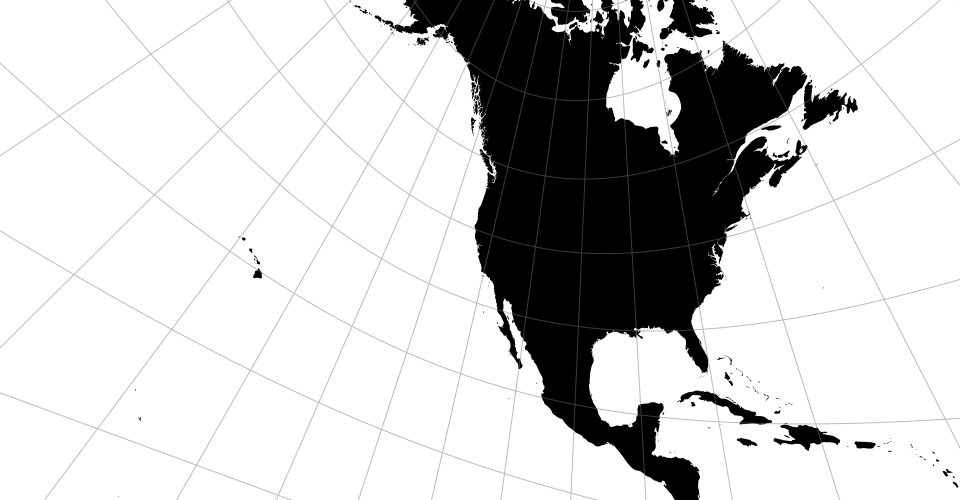
A modified stereographic projection for Alaska.

# d3.geoModifiedStereographicGs48() · Source

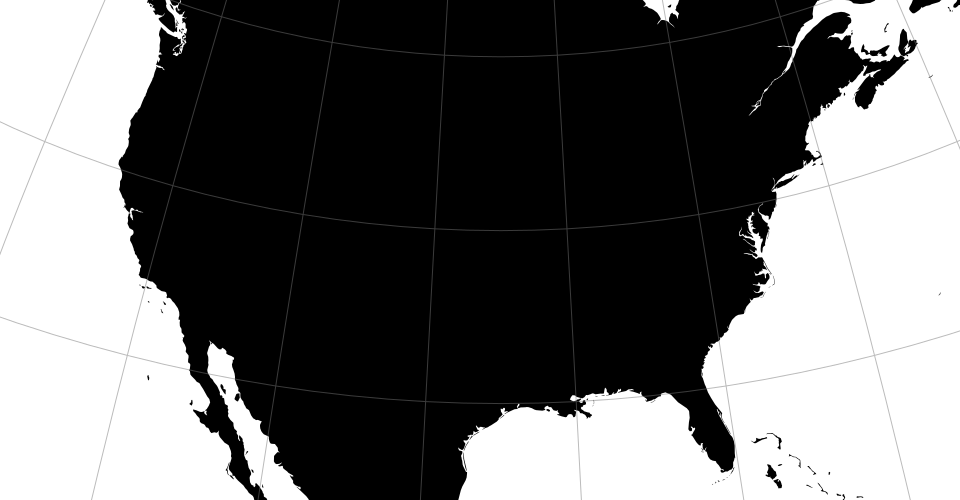
A modified stereographic projection for the conterminous United States.

# d3.geoModifiedStereographicGs50() · Source

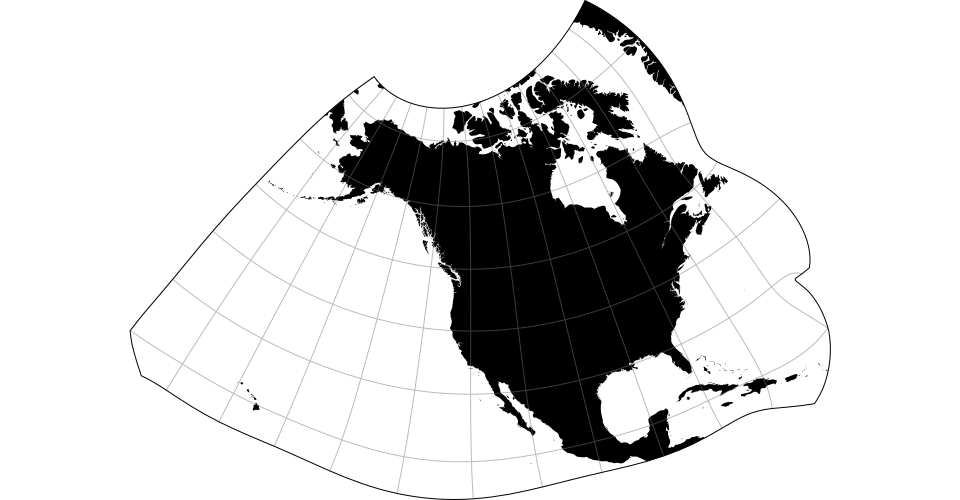
A modified stereographic projection for the United States including Alaska and Hawaii. Typically clipped to the geographic extent [[-180°, 15°], [-50°, 75°]].

# d3.geoModifiedStereographicMiller() · Source, Examples

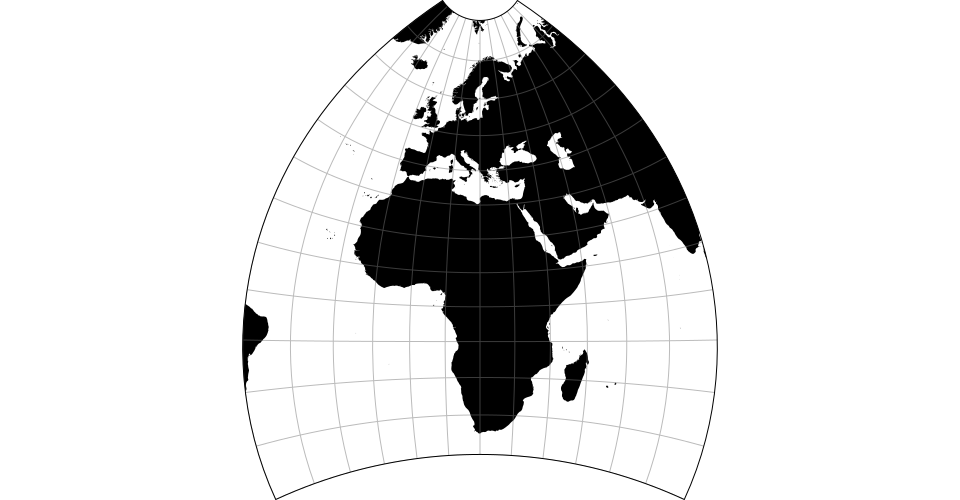
A modified stereographic projection for Europe and Africa. Typically clipped to the geographic extent [[-40°, -40°], [80°, 80°]].

# d3.geoModifiedStereographicLee() · Source, Examples

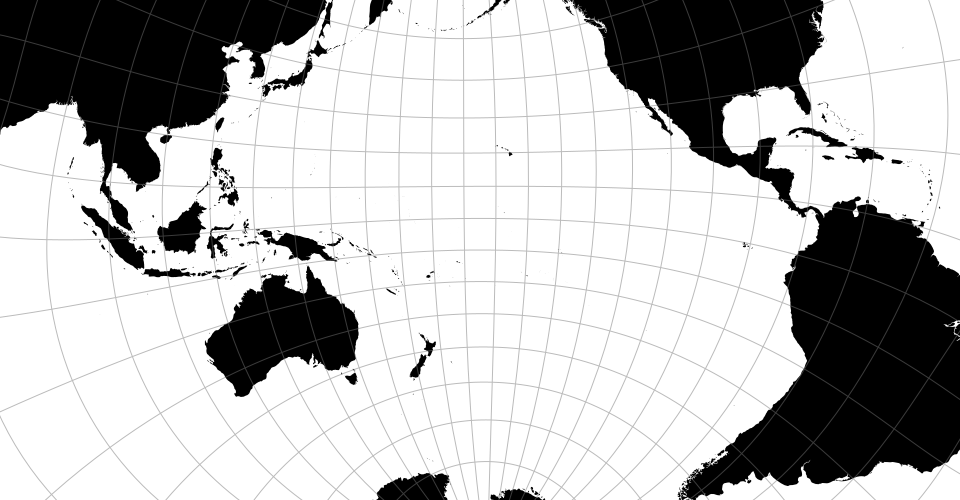
A modified stereographic projection for the Pacific ocean.

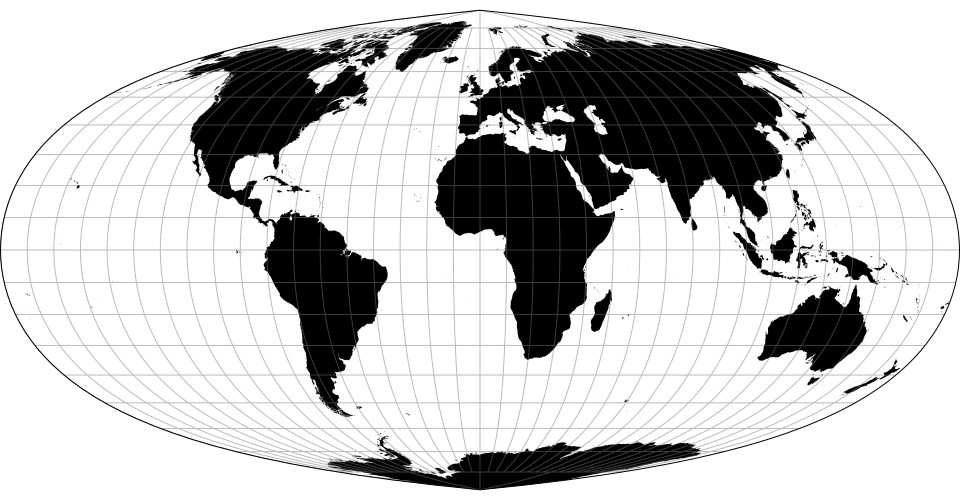
# d3.geoMollweide() · Source, Examples
# d3.geoMollweideRaw

The equal-area, pseudocylindrical Mollweide projection. The oblique aspect is known as the Atlantis projection. Goode’s interrupted Mollweide is also widely known.

# d3.geoMtFlatPolarParabolic() · Source, Examples
# d3.geoMtFlatPolarParabolicRaw

The McBryde–Thomas flat-polar parabolic pseudocylindrical equal-area projection.

# d3.geoMtFlatPolarQuartic() · Source, Examples
# d3.geoMtFlatPolarQuarticRaw

The McBryde–Thomas flat-polar quartic pseudocylindrical equal-area projection.

# d3.geoMtFlatPolarSinusoidal() · Source, Examples
# d3.geoMtFlatPolarSinusoidalRaw

The McBryde–Thomas flat-polar sinusoidal equal-area projection.

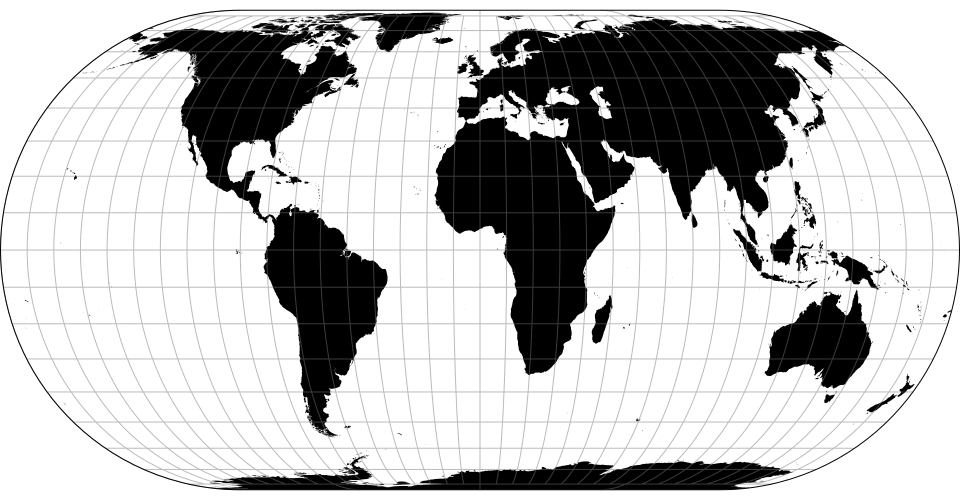
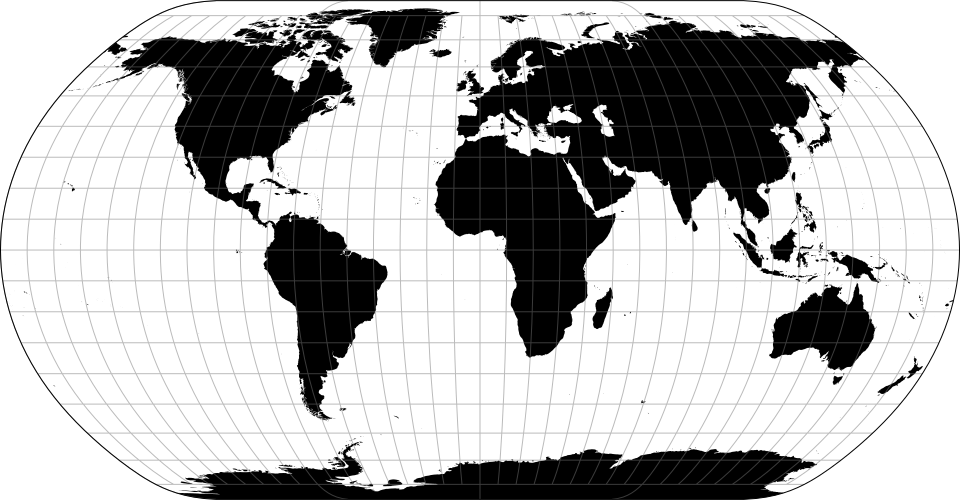
# d3.geoNaturalEarth1() · Source [d3-geo], Examples
# d3.geoNaturalEarth1Raw

The Natural Earth projection.

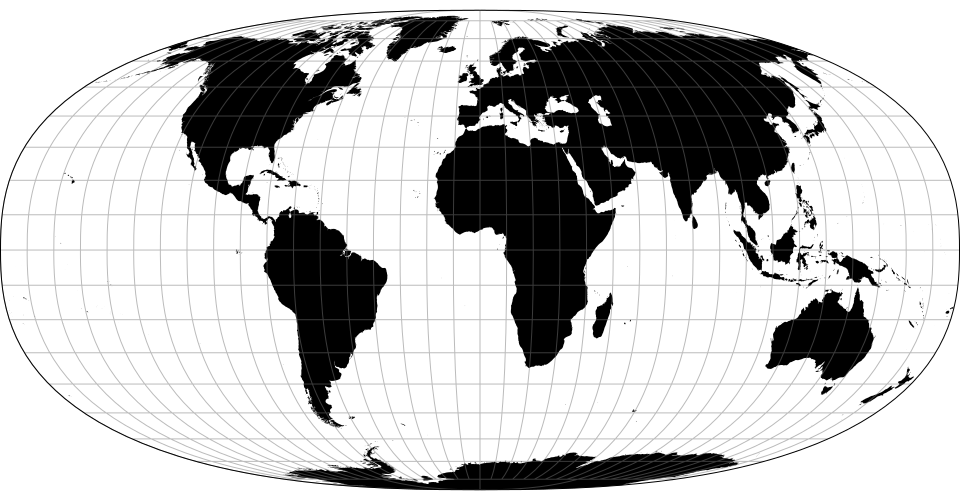
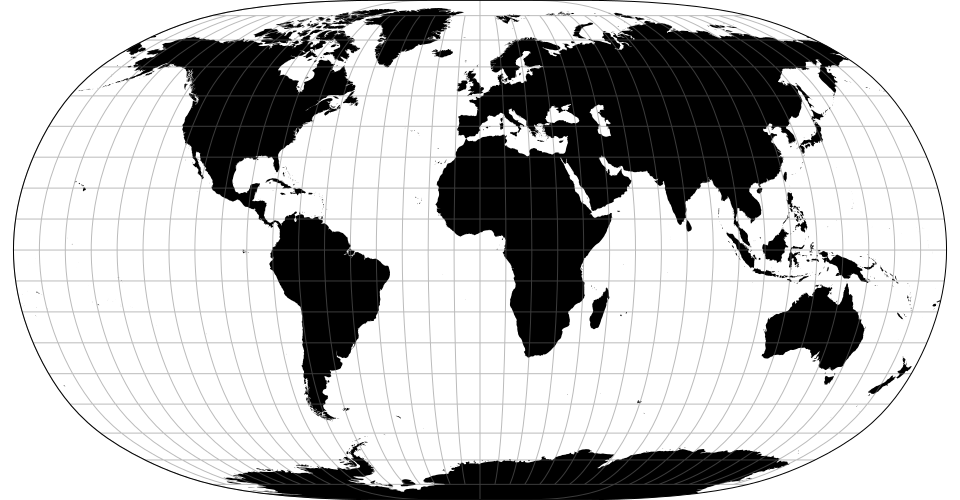
# d3.geoNaturalEarth2() · Source, Examples
# d3.geoNaturalEarth2Raw

The Natural Earth II projection. Compared to Natural Earth, it is slightly taller and rounder.

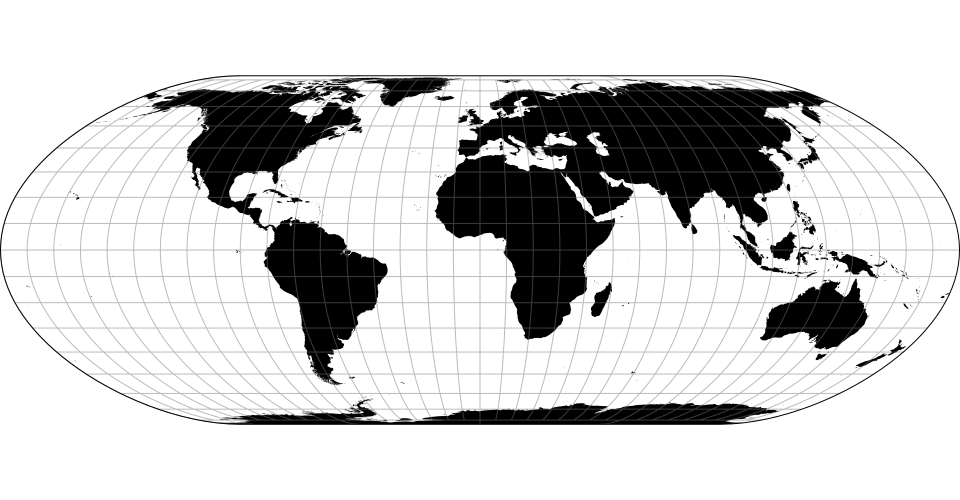
# d3.geoNellHammer() · Source, Examples
# d3.geoNellHammerRaw

The Nell–Hammer projection.

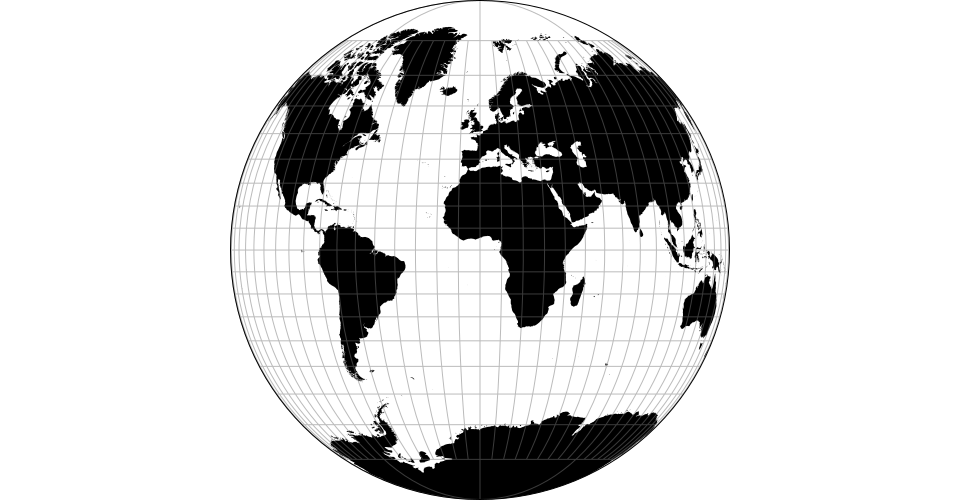
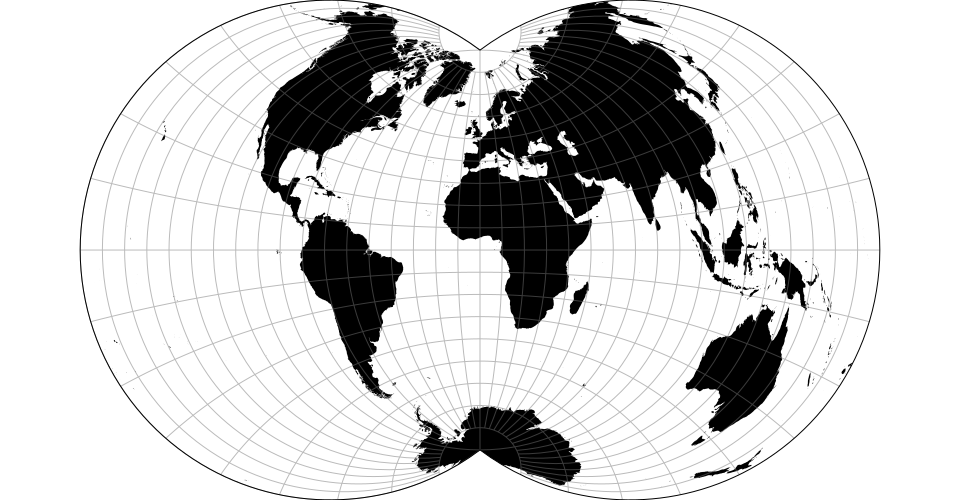
# d3.geoNicolosi() · Source, Examples
# d3.geoNicolosiRaw

The Nicolosi globular projection.

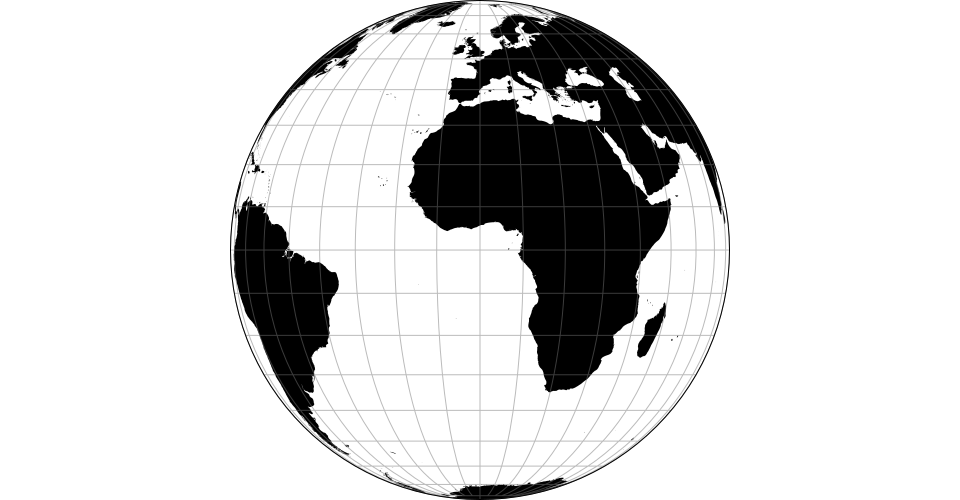
# d3.geoOrthographic() · Source [d3-geo], Examples
# d3.geoOrthographicRaw

The orthographic projection.

# d3.geoPatterson() · Source, Examples
# d3.geoPattersonRaw

The Patterson cylindrical projection.

# d3.geoPolyconic() · Source, Examples
# d3.geoPolyconicRaw

The American polyconic projection.

# d3.geoRectangularPolyconic() · Source, Examples
# d3.geoRectangularPolyconicRaw(phi0)

The rectangular (War Office) polyconic projection.

# rectangularPolyconic.parallel([parallel])

Defaults to 0°.

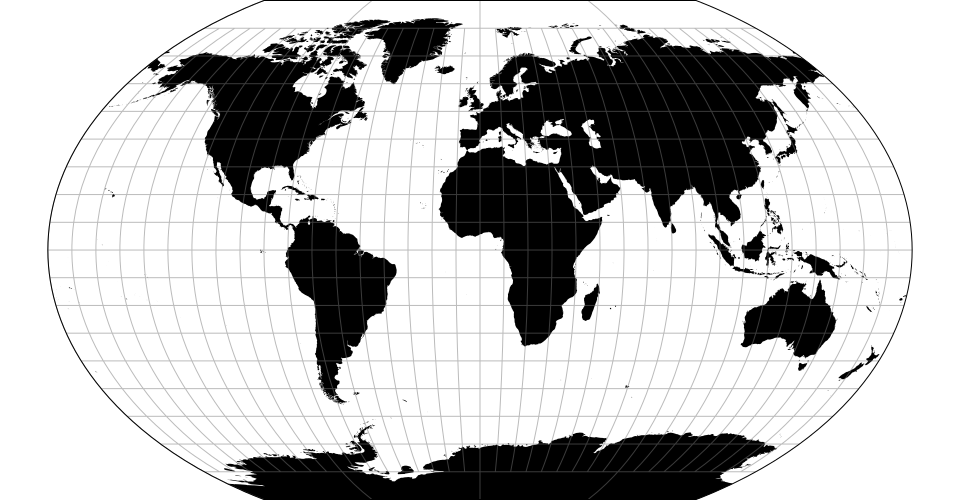
# d3.geoRobinson() · Source, Examples
# d3.geoRobinsonRaw

The Robinson projection.

# d3.geoSatellite() · Source, Examples
# d3.geoSatelliteRaw(P, omega)

The satellite (tilted perspective) projection.

# satellite.tilt([tilt])

Defaults to 0°.

# satellite.distance([distance])

Distance from the center of the sphere to the point of view, as a proportion of the sphere’s radius; defaults to 2.0. The recommended maximum clip angle for a given distance is acos(1 / distance) converted to degrees. If tilt is also applied, then more conservative clipping may be necessary. For exact clipping, the in-development geographic projection pipeline is needed; see the satellite explorer.

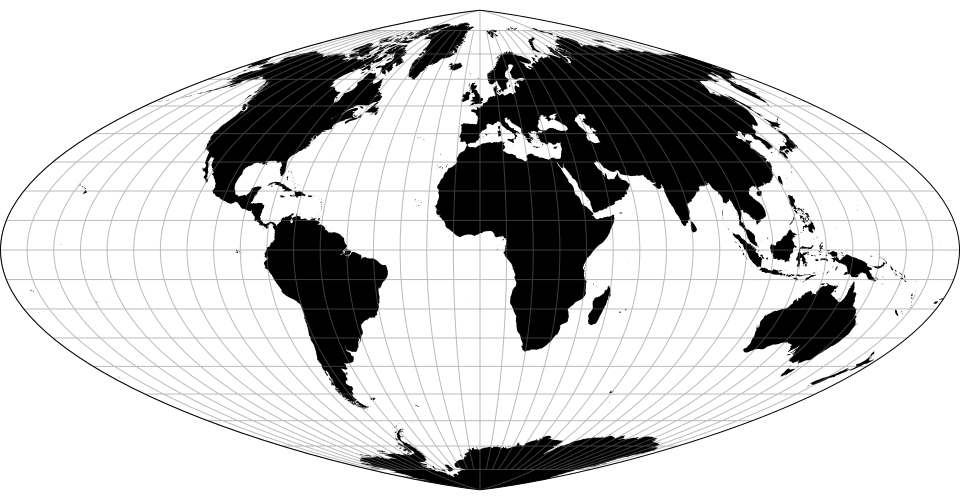
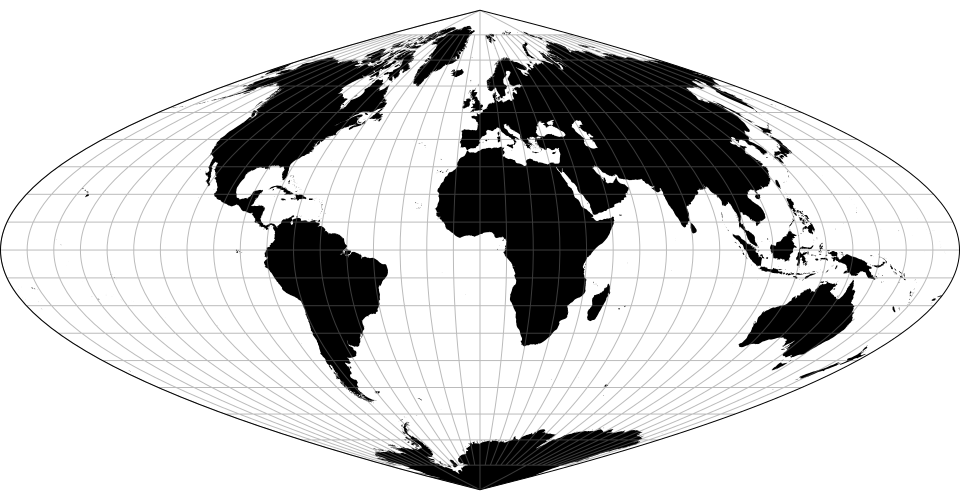
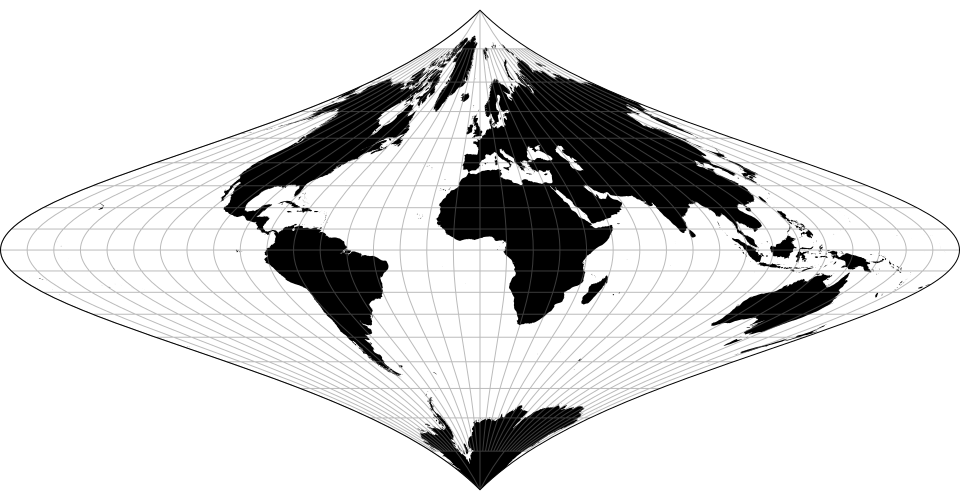
# d3.geoSinusoidal() · Source, Examples
# d3.geoSinusoidalRaw

The sinusoidal projection.

# d3.geoSinuMollweide() · Source, Examples
# d3.geoSinuMollweideRaw

Allen K. Philbrick’s Sinu-Mollweide projection. See also the interrupted form.

# d3.geoStereographic() · Source [d3-geo], Examples
# d3.geoStereographicRaw

The stereographic projection.

# d3.geoTimes() · Source, Examples
# d3.geoTimesRaw

John Muir’s Times projection.

# d3.geoTransverseMercator() · Source [d3-geo], Examples
# d3.geoTransverseMercatorRaw

The transverse spherical Mercator projection.

# d3.geoTwoPointAzimuthal(point0, point1) · Source
# d3.geoTwoPointAzimuthalRaw(d)

The two-point azimuthal projection “shows correct azimuths (but not distances) from either of two points to any other point. [It can] be used to locate a ship at sea, given the exact location of two radio transmitters and the direction of the ship to the transmitters.” This projection does not support projection.rotate, as the rotation is fixed by the two given points.

# d3.geoTwoPointAzimuthalUsa() · Source

The two-point azimuthal projection with points [-158°, 21.5°] and [-77°, 39°], approximately representing Honolulu, HI and Washington, D.C.

# d3.geoTwoPointEquidistant(point0, point1) · Source
# d3.geoTwoPointEquidistantRaw(z0)

The two-point equidistant projection. This projection does not support projection.rotate, as the rotation is fixed by the two given points. Note: to show the whole Earth, this projection requires clipping to spherical polygons (example).

# d3.geoTwoPointEquidistantUsa() · Source

The two-point equidistant projection with points [-158°, 21.5°] and [-77°, 39°], approximately representing Honolulu, HI and Washington, D.C.

# d3.geoVanDerGrinten() · Source, Examples
# d3.geoVanDerGrintenRaw

The Van der Grinten projection.

# d3.geoVanDerGrinten2() · Source, Examples
# d3.geoVanDerGrinten2Raw

The Van der Grinten II projection.

# d3.geoVanDerGrinten3() · Source, Examples
# d3.geoVanDerGrinten3Raw

The Van der Grinten III projection.

# d3.geoVanDerGrinten4() · Source, Examples
# d3.geoVanDerGrinten4Raw

The Van der Grinten IV projection.

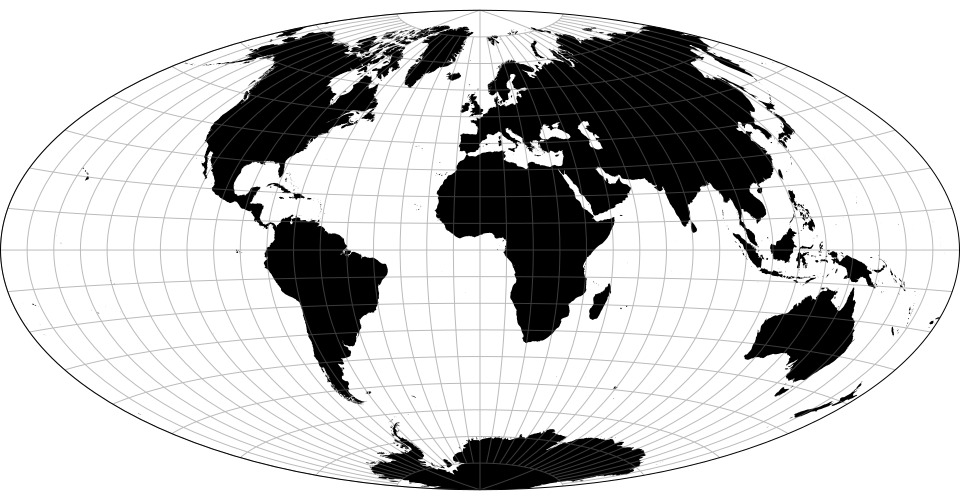
# d3.geoWagner() · Source, Examples
# d3.geoWagnerRaw

The Wagner projection is customizable: default values produce the Wagner VIII projection.

# wagner.poleline([poleline])

Defaults to 65°.

# wagner.parallels([parallels])

Defaults to 60°.

# wagner.inflation([inflation])

Defaults to 20.

# wagner.ratio([ratio])

Defaults to 200.

# d3.geoWagner4() · Source, Examples
# d3.geoWagner4Raw

The Wagner IV projection, also known as Putniṇš P2´.

# d3.geoWagner6() · Source, Examples
# d3.geoWagner6Raw

The Wagner VI projection.

# d3.geoWagner7() · Source, Examples

The Wagner VII projection.

# d3.geoWiechel() · Source, Examples
# d3.geoWiechelRaw

The Wiechel projection.

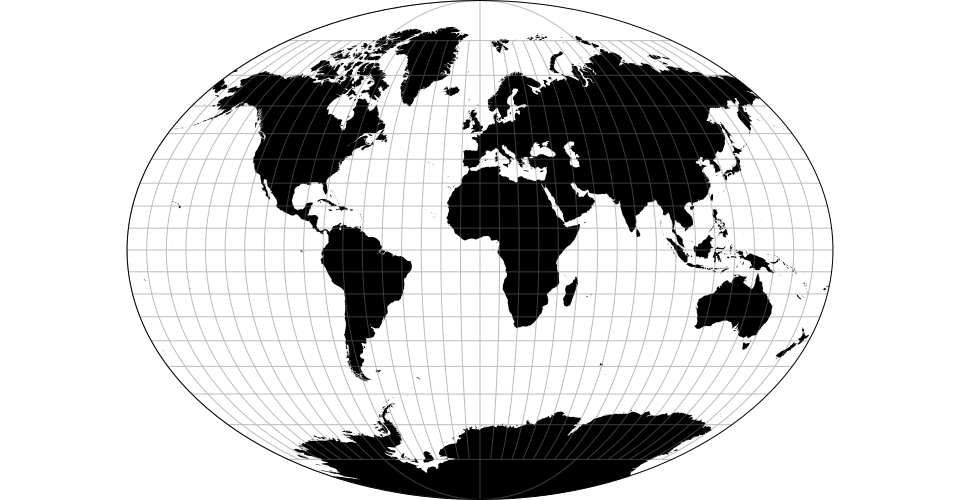
# d3.geoWinkel3() · Source, Examples
# d3.geoWinkel3Raw

The Winkel tripel projection.

Interrupted Projections

# d3.geoInterrupt(project, lobes) · Source, Examples

Defines a new interrupted projection for the specified raw projection function project and the specified array of lobes. The array lobes contains two elements representing the hemilobes for the northern hemisphere and the southern hemisphere, respectively. Each hemilobe is an array of triangles, with each triangle represented as three points (in degrees): the start, midpoint, and end. For example, the lobes in Goode’s interrupted homolosine projection are defined as:

[
  [
    [[-180,   0], [-100,  90], [ -40,   0]],
    [[ -40,   0], [  30,  90], [ 180,   0]]
  ],
  [
    [[-180,   0], [-160, -90], [-100,   0]],
    [[-100,   0], [ -60, -90], [ -20,   0]],
    [[ -20,   0], [  20, -90], [  80,   0]],
    [[  80,   0], [ 140, -90], [ 180,   0]]
  ]
]

Note: interrupted projections typically require clipping to the sphere.

# interrupted.lobes([lobes]) · Source

If lobes is specified, sets the new array of hemilobes and returns this projection; see d3.geoInterrupt for details on the format of the hemilobes array. If lobes is not specified, returns the current array of hemilobes.

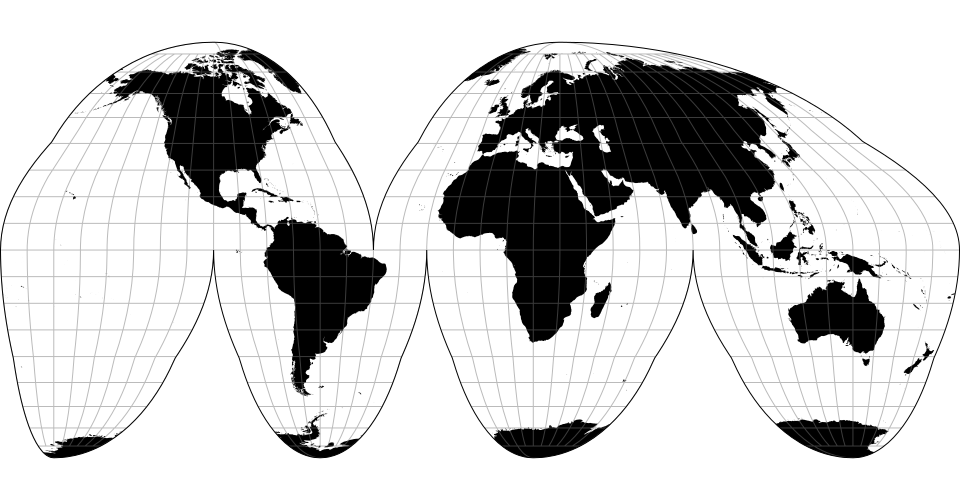
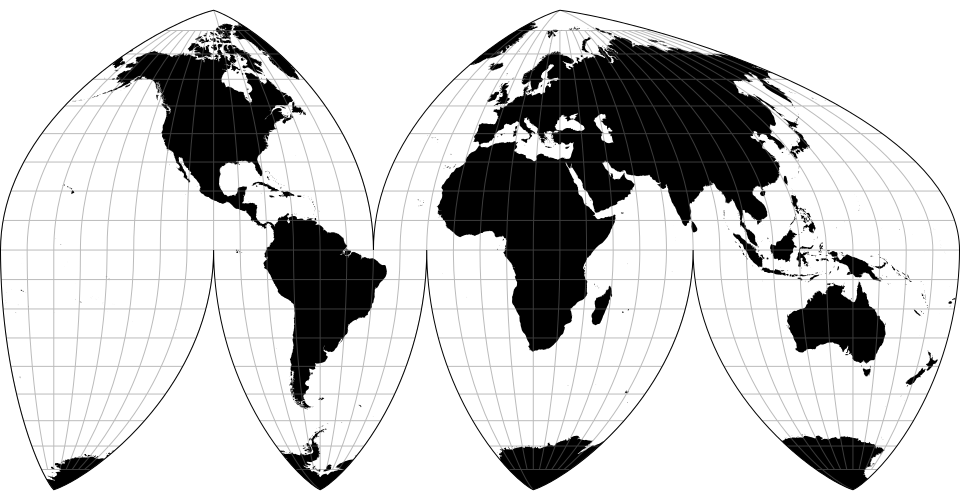
# d3.geoInterruptedHomolosine() · Source, Examples

Goode’s interrupted homolosine projection. Its ocean-centric aspect is also well-known.

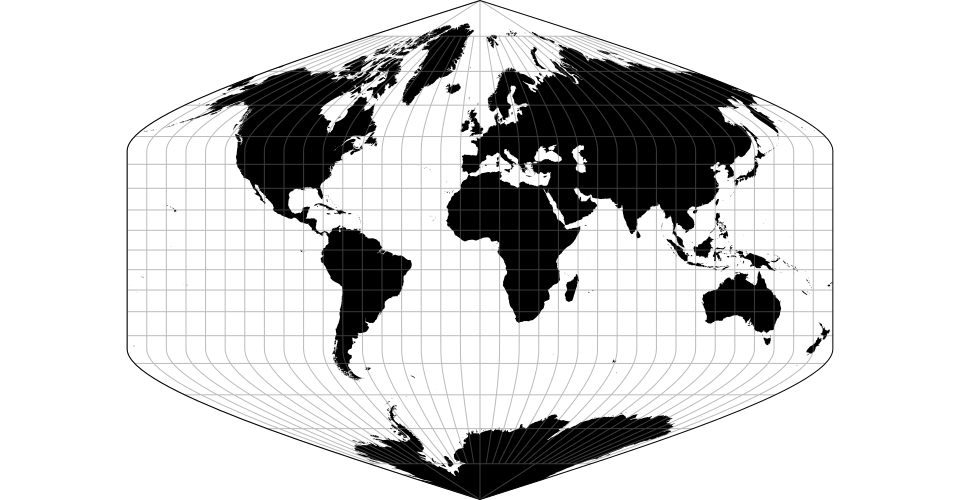
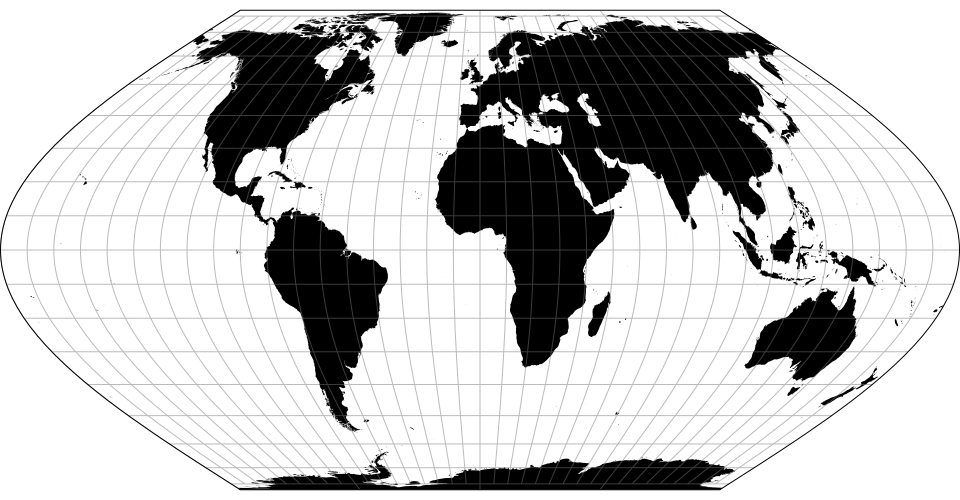
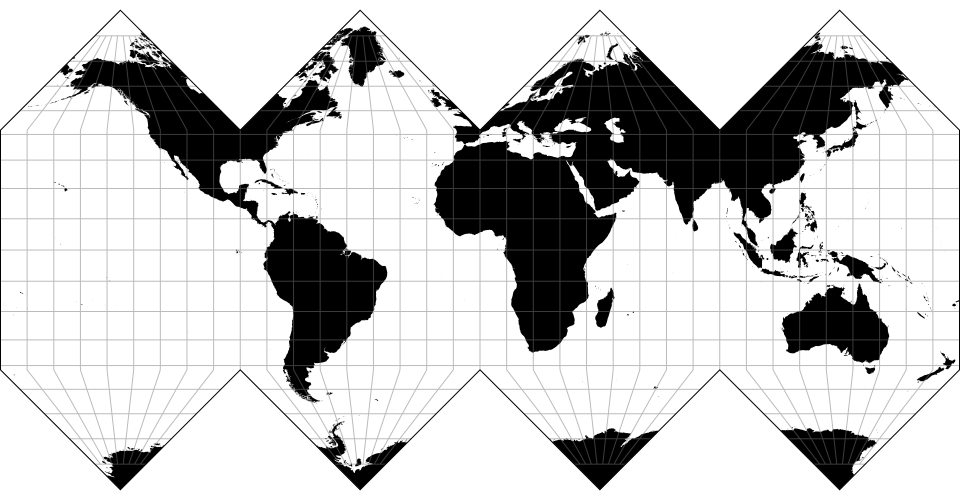
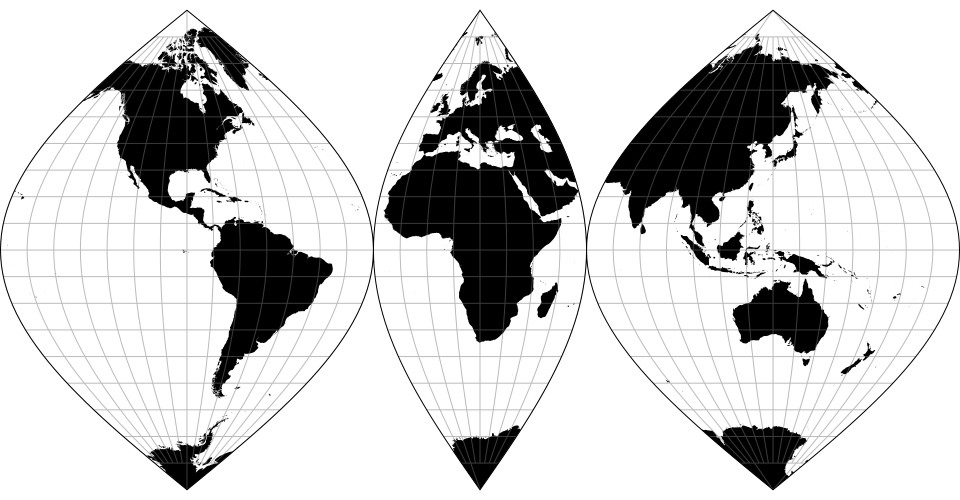
# d3.geoInterruptedSinusoidal() · Source, Examples

An interrupted sinusoidal projection with asymmetrical lobe boundaries that emphasize land masses over oceans, after the Swedish Nordisk Världs Atlas as reproduced by C.A. Furuti.

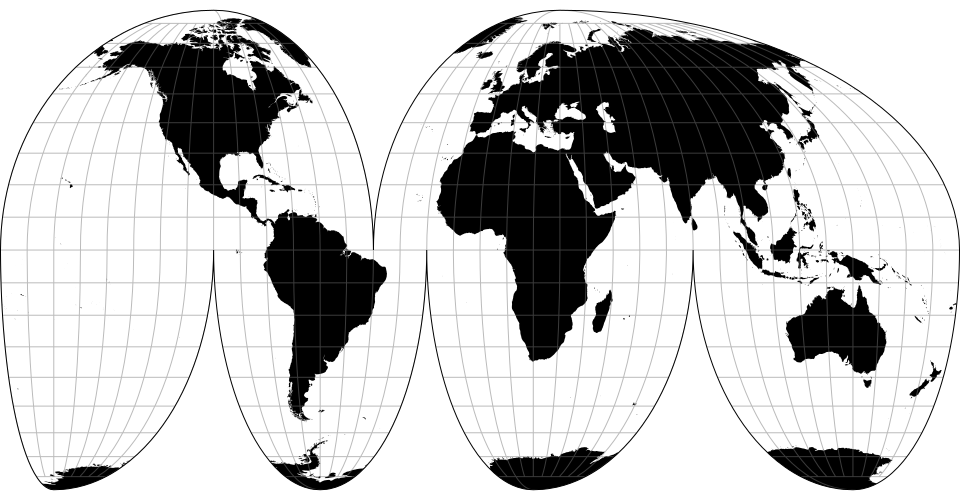
# d3.geoInterruptedBoggs() · Source, Examples

Bogg’s interrupted eumorphic projection.

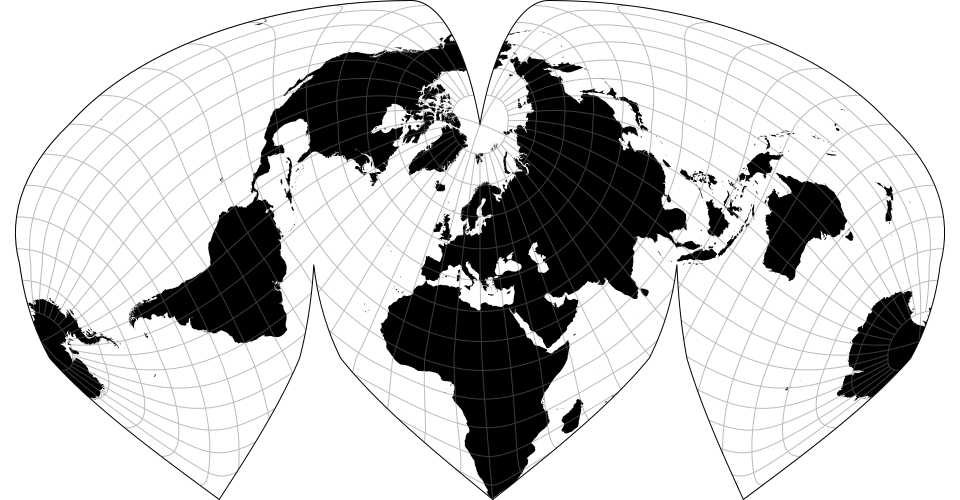
# d3.geoInterruptedSinuMollweide() · Source, Examples

Alan K. Philbrick’s interrupted sinu-Mollweide projection.

# d3.geoInterruptedMollweide() · Source, Examples

Goode’s interrupted Mollweide projection.

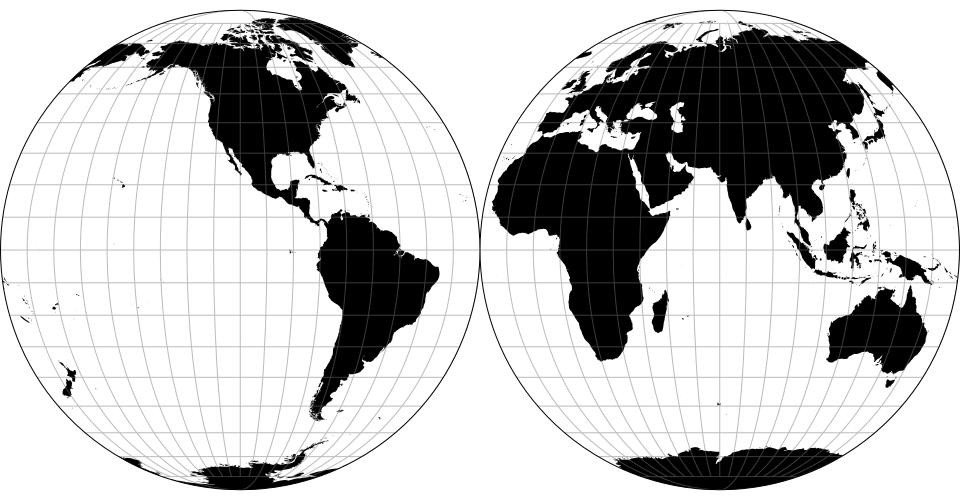
# d3.geoInterruptedMollweideHemispheres() · Source, Examples

The Mollweide projection interrupted into two (equal-area) hemispheres.

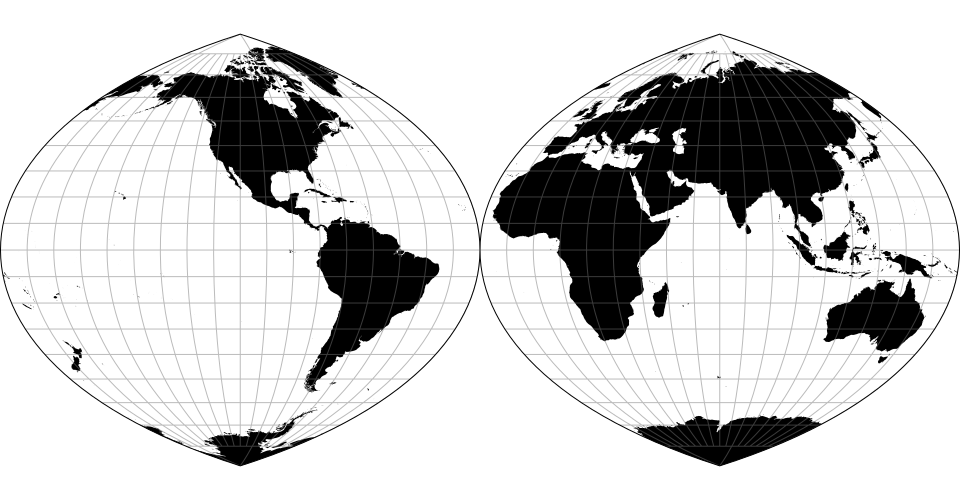
# d3.geoInterruptedQuarticAuthalic() · Source, Examples

The quartic authalic projection interrupted into two hemispheres.

Polyhedral Projections

# d3.geoPolyhedral(root, face) · Source

Defines a new polyhedral projection. The root is a spanning tree of polygon face nodes; each node is assigned a node.transform matrix. The face function returns the appropriate node for a given lambda and phi in radians. Use projection.angle to set the orientation of the map (the default angle, -30°, might change in the next major version).

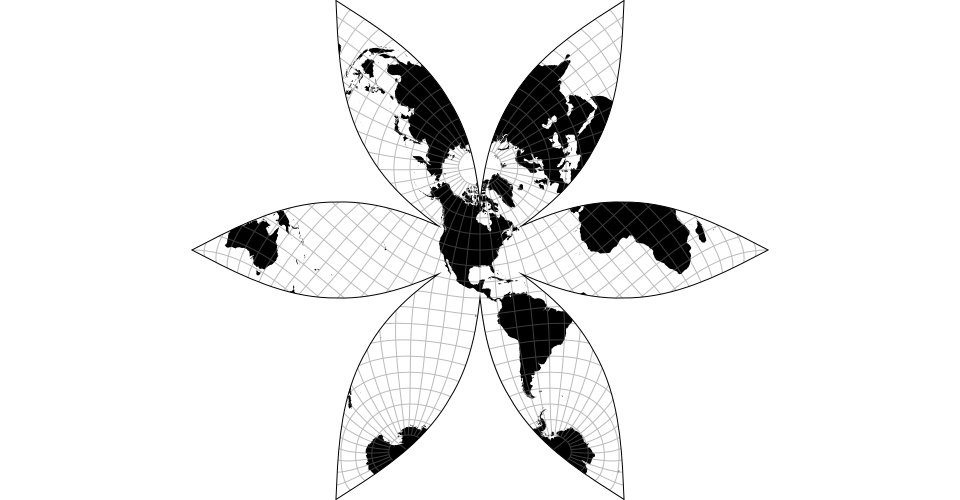
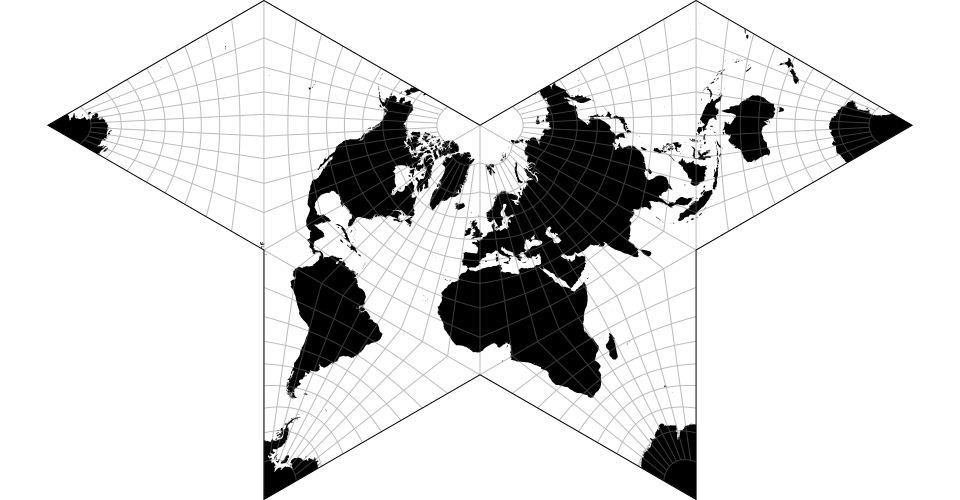
# d3.geoPolyhedralButterfly() · Source, Examples

The gnomonic butterfly projection.

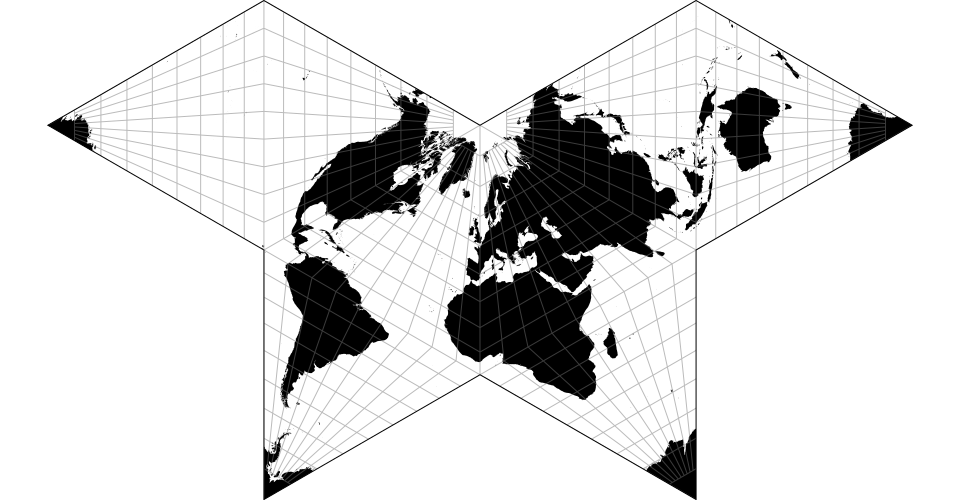
# d3.geoPolyhedralCollignon() · Source, Examples

The Collignon butterfly projection.

# d3.geoPolyhedralWaterman() · Source, Examples

Steve Waterman’s butterfly projection.

Quincuncial Projections

# d3.geoQuincuncial(project) · Source

Defines a new quincuncial projection for the specified raw projection function project. The default rotation is [-90°, -90°, 45°] and the default clip angle is 180° - ε.

# d3.geoGringortenQuincuncial() · Source, Examples

The Gringorten square equal-area projection.

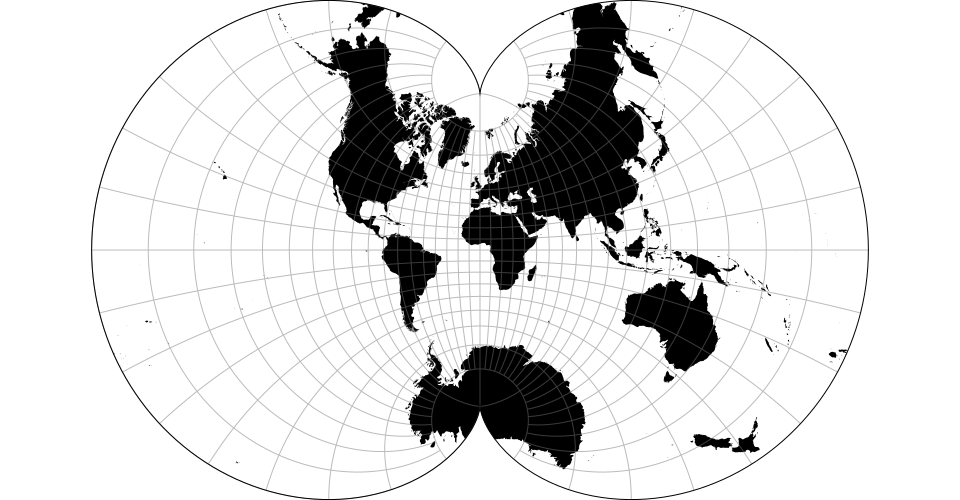
# d3.geoPeirceQuincuncial() · Source

The Peirce quincuncial projection is the quincuncial form of the Guyou projection.

Transformations

# d3.geoProject(object, projection) · Source

Projects the specified GeoJSON object using the specified projection, returning a shallow copy of the specified GeoJSON object with projected coordinates. Typically, the input coordinates are spherical and the output coordinates are planar, but the projection can also be an arbitrary geometric transformation.

Command-Line Reference

geo2svg

# geo2svg [options…] [file] · Source

Converts the specified GeoJSON file to SVG. With --newline-delimited, each input feature is rendered as a separate path element; otherwise, a single path element is generated.

By default, the SVG’s fill is set to none and the stroke is set to black. The default point radius is 4.5. To override these values on a per-feature basis, the following GeoJSON feature properties will be propagated to attributes:

fill
fill-rule (or fillRule)
fill-opacity (or fillOpacity)
stroke
stroke-width (or strokeWidth)
stroke-linecap (or strokeLinecap)
stroke-linejoin (or strokeLinejoin)
stroke-miterlimit (or strokeMiterlimit)
stroke-dasharray (or strokeDasharray)
stroke-dashoffset (or strokeDashoffset)
stroke-opacity (or strokeOpacity)
point-radius (or pointRadius)

If the feature has an id, the path element will have a corresponding id attribute. If the feature has a title property, the path element will have a title element with the corresponding value. For an example of per-feature attributes, see this California population density map.

Note: per-feature attributes are most useful in conjunction with newline-delimited input, as otherwise the generated SVG only has a single path element. To set these properties dynamically, pass the input through ndjson-map.

# geo2svg -h
# geo2svg --help

Output usage information.

# geo2svg -V
# geo2svg --version

Output the version number.

# geo2svg -o file
# geo2svg --out file

Specify the output file name. Defaults to “-” for stdout.

# geo2svg -w value
# geo2svg --width value

Specify the output width. Defaults to 960.

# geo2svg -h value
# geo2svg --height value

Specify the output height. Defaults to 500.

# geo2svg -p value
# geo2svg --precision value

Reduce the precision for smaller output files. Defaults to six digits after the decimal point. See also d3.geoQuantize.

# geo2svg --fill value

Specify the default output fill color. Defaults to none.

# geo2svg --stroke value

Specify the default output stroke color. Defaults to black.

# geo2svg --r value
# geo2svg --radius value

Specify the default output point radius. Defaults to 4.5.

# geo2svg -n
# geo2svg --newline-delimited

Accept newline-delimited JSON as input, with one feature per line.

geograticule

# geograticule [options…] · Source

Generates a GeoJSON graticule. See also d3.geoGraticule.

# geograticule -h
# geograticule --help

Output usage information.

# geograticule -V
# geograticule --version

Output the version number.

# geograticule -o file
# geograticule --out file

Specify the output file name. Defaults to “-” for stdout.

# geograticule --extent value

Sets the graticule’s extent.

# geograticule --extent-minor value

Sets the graticule’s minor extent.

# geograticule --extent-major value

Sets the graticule’s major extent.

# geograticule --step value

Sets the graticule’s step.

# geograticule --step-minor value

Sets the graticule’s minor step.

# geograticule --step-major value

Sets the graticule’s major setp.

# geograticule --precision value

Sets the graticule’s precision.

geoproject

# geoproject [options…] projection [file] · Source

Projects the GeoJSON object in the specified input file using the specified projection, outputting a new GeoJSON object with projected coordinates. For example, to project standard WGS 84 input using d3.geoAlbersUsa:

geoproject 'd3.geoAlbersUsa()' us.json \
  > us-albers.json

For geometry that crosses the antimeridian or surrounds a pole, you will want to pass input through geostitch first:

geostitch world.json \
  | geoproject 'd3.geoMercator()' \
  > world-mercator.json

Typically, the input coordinates are spherical and the output coordinates are planar, but the projection can also be an arbitrary geometric transformation. For example, to invert the y-axis of a standard spatial reference system such as California Albers (EPSG:3310) and fit it to a 960×500 viewport:

shp2json planar.shp \
  | geoproject 'd3.geoIdentity().reflectY(true).fitSize([960, 500], d)' \
  > planar.json

See also d3.geoProject and d3.geoIdentity.

# geoproject -h
# geoproject --help

Output usage information.

# geoproject -V
# geoproject --version

Output the version number.

# geoproject -o file
# geoproject --out file

Specify the output file name. Defaults to “-” for stdout.

# geoproject -p value
# geoproject --precision value

Reduce the precision for smaller output files. See also d3.geoQuantize.

# geoproject -n
# geoproject --newline-delimited

Accept newline-delimited JSON as input, with one feature per line, and generate newline-delimited JSON as output.

# geoproject -r [name=]value
# geoproject --require [name=]value

Requires the specified module, making it available for use in any expressions used by this command. The loaded module is available as the symbol name. If name is not specified, it defaults to module. (If module is not a valid identifier, you must specify a name.) For example, to reproject the world on the Airocean projection:

geoproject --require d3=d3-geo-polygon 'd3.geoAirocean()' world.geojson

The required module is resolved relative to the current working directory. If the module is not found during normal resolution, the global npm root is also searched, allowing you to require globally-installed modules from the command line.

Multiple modules can be required by repeating this option.

geoquantize

# geoquantize [options…] [file] · Source

Reads the GeoJSON object from the specified input file and outputs a new GeoJSON object with coordinates reduced to precision. Same options as geoproject.

geoquantize us.json --precision 3 \
  > us-quantized.json

geostitch

# geostitch [options…] [file] · Source

Stitches the GeoJSON object in the specified input file, removing antimeridian and polar cuts, and replacing straight Cartesian line segments with geodesic segments. The input object must have coordinates in longitude and latitude in decimal degrees per RFC 7946. Antimeridian cutting, if needed, can then be re-applied after rotating to the desired projection aspect.

See geoproject for an example. See also d3.geoStitch.

# geostitch -h
# geostitch --help

Output usage information.

# geostitch -V
# geostitch --version

Output the version number.

# geostitch -o file
# geostitch --out file

Specify the output file name. Defaults to “-” for stdout.

# geostitch -n
# geostitch --newline-delimited

Accept newline-delimited JSON as input, with one feature per line, and generate newline-delimited JSON as output.

d3-geo-projection's People

Contributors

Stargazers

Watchers

Forkers

thiagoaslima wonderwoob jaspervdg zebramind geometeor radiodario imclab aciil yl588 vyrak handerlo olivoil anoopbhargava tchen0123 i17c emcpadden timlinux indian2020 mark-hoo sludge1 vlux marc-white thdtjsdn vasile andreabadesso cs-ozgur itdonline jorgml miladghaznavi taeyoung-yoon ofrohn jhollist sweetymeow admackin cnh liqianggao thewiremonkey mihai cambecc imanavaz etpinard kurcias datanalyst gerhobbelt emilbayes adityavs dr-mokhless jswiss simaq paulkoegel tosseto jsheedy nacholopezd3js danhostetler rasata kiernanmcgowan gordonsmith adamhooper gaubert stacy779 epicallan tangdru mingyu-lee quickhand chrisuehlinger jx2011 torbenjansen rlugojr jackaiwang fil cuulee mariacrosas hooperzao digideskio javascriptextjs diniden martgnz reverland rveciana brijesh333 terratenney lpk-py jbarn080 pk-codebox-evo madhanrd apezel zdong1 xwu-ut woodymax mthh tinius sangkyunyoon yyu anbnyc xuluxi macro-shen i-am-ironman gregorynicholas johnburnmurdoch aendra-rininsland

d3-geo-projection's Issues

Natural Earth II?

http://www.shadedrelief.com/NE2_proj/

Add Foucaut preview to the README.

Better aspect ratios for HEALPix when lobes != 4.

Kinda gets too wide.

Dymaxion projection?

The Dymaxion map projection would be utterly awesome :)

d3.geoProject

This was somewhat inadvertently removed in the 1.0 release. The implementation is arguably buggy in that it doesn’t preserve polygon semantics, but I will need this method to upgrade topojson to D3 4.1. Possibly it could be in a separate repository.

D3 Geo doesn't work with browserify

Document geoProject and geoStitch.

geoscale

It’d be nice to have a binary for taking projected, planar GeoJSON as input and then transforming the coordinates to fit the specified bounding box. It should also support --invert for flipping the y-dimension, as Proj4 and other projection systems typically use the other y direction than Canvas and SVG.

https://github.com/topojson/topojson/blob/v1.6.27/lib/topojson/scale.js

Register with bower.

Algorithmic search for inverse projections

It would be nice to be able to fall back on an algorithmic search (Newton-Raphson) when inverse isn't defined, for any projection.

Several inverse projections already do this, but it's not centralized (example: https://github.com/d3/d3-geo-projection/search?q=Newton-Raphson).

Related:
#70
d3/d3-geo#69 (comment)

advice needed

your d3-geo-projections look super interesting.

i usually develop with c++ and use the openframework.cc libraries.
i was hoping to use your geographic projections code posted here in my project.

while i am mostly able to translate your code in to c++ i am not sure how your call your different projection functions and build a map from them.

do you pass in 360˚ values for λ and φ do represent the whole globe/ sphere?

here is how i translated eckert1.

ofPoint ofApp::eckert1(float λ,float φ) {
    //https://github.com/d3/d3-geo-projection/blob/master/src/eckert1.js
    float α = sqrt(8 / (3 * PI));
    return ofPoint(α * λ * (1 - abs(φ) / PI),α * φ);
}

ofPoint ofApp::eckert1_invert(float x,float y) {
    float α = sqrt(8 / (3 * PI));
    float φ = y / α;
    return ofPoint(x / (α * (1 - abs(φ) / PI)),φ);
};

i say mostly able because for example i am not sure what ε epsilon stands for in naturalEarth.invert function.

thanks for any advice.
stephan.

Document new command-line tools.

Bring more consistency to the API

I wonder if the raw projections should not all be added as generators in the raw or rawgenerator property of the projection. This would make them consistent and discoverable. Currently there is no easy way to remember is the xxxRaw is a projection generator or a projection — one has to look up README.md.

Also wonder if the documentation of each projection should not be added to src/{projection}.js, from which we could build the README.md.

Not to slow down release of 1.0!

geograticule

When creating projected TopoJSON, it’d be handy to generate and bake a graticule or sphere into the generated Topology. (It’s now possible to use echo '{"type": "Sphere"} | geoproject` so we don’t really need sphere creation.)

Moved from topojson/topojson#157.

geostitch --segment?

Some GIS (GISes?) assume linear interpolation, even in spherical coordinate systems such as WGS84 / EPSG:4326. This is bad because it is rotation-variant. In contrast, D3 / TopoJSON assume great arcs (spherical interpolation) between points on lines and rings in spherical coordinates.

It would be useful if TopoJSON had a built-in way to fix this assumption as part of the conversion process, introducing interstitial points. Ideally this would be adaptive and measure the deviation between the great arc and the Cartesian line, but here is a simple approach that could then be simplified to achieve the same result:

// Takes a sparse line string that assumes Cartesian interpolation in spherical
// coordinates and inserts interstitial points for greater accuracy when
// rendering with D3, which assumes spherical interpolation.
function resample(coordinates) {
  var i = 0,
      j = -1,
      n = coordinates.length,
      source = coordinates.slice(),
      p0, x0, y0,
      p1 = coordinates[0], x1 = p1[0], y1 = p1[1],
      dx, dy, d2,
      m2 = 10; // squared minimum angular distance
  while (++i < n) {
    p0 = p1, x0 = x1, y0 = y1;
    p1 = source[i], x1 = p1[0], y1 = p1[1];
    dx = x1 - x0, dy = y1 - y0, d2 = dx * dx + dy * dy;
    coordinates[++j] = p0;
    if (d2 > m2) for (var k = 1, m = Math.ceil(Math.sqrt(d2 / m2)); k < m; ++k) {
      coordinates[++j] = [x0 + dx * k / m, y0 + dy * k / m];
    }
  }
  coordinates[++j] = p1;
  coordinates.length = j + 1;
}

I’m not sure whether we want to assume that GeoJSON / Shapefile input assumes linear interpolation in spherical coordinates, or if we only want to enable this selectively using a command-line argument. Probably the latter is the safer course of action, although I suspect many users are not aware of this issue.

Moved from topojson/topojson#110.

Fix all invert projections

Except those that can't be fixed, maybe.

The list of broken invert projections is given by the lines that are commented out in https://github.com/d3/d3-geo-projection/blob/master/test/invert-test.js

Noob questions

I'm interested in creating a projection for d3 that works with the s2 library co-ordinates from google https://docs.google.com/presentation/d/1Hl4KapfAENAOf4gv-pSngKwvS_jwNVHRPZTTDzXXn6Q/view#slide=id.i0

Things I'd like to try is rendering the earth out as a cube, using the 3 mentioned methods of linear / tangent / quadratic, as well as rendering stored s2 cells onto various projections.

What would be the basic pre-requisite knowledge that I would need to start?

How would you go about handling existing terrain / tile maps not made for this projection?

One thing I'm concerned about is performance, maybe past a certain zoom level I should drop back to a flat plane representing a cube face rather then doing all the projection math? How smooth would it be to transition between them?

Repoint bower to mbostock-bower/d3-geo-projection-bower.

So that we can remove the generated files and prepare for D3 4.0.

polyhedron.waterman projection clearly differs from waterman’s version

This version seems to just be a Gnomonic projection on particular sections, while Waterman’s own projection is something different. (I can’t actually figure out what the technical details are on Waterman’s version.) The easiest place to see the difference is in the shape of the parallels near the poles. On a globe or azimuthal projection centered on a pole, these are shaped like quarter circles. In the d3/Gnomonic version, they are stretched toward the center. By contrast, in Waterman’s projection, the middle of each quarter circle is squished toward poles.

I highly recommend adding an explicit disclaimer that this is not actually Waterman’s projection per se. Ideally it would be possible to ask Waterman for the details and implement the projection properly. Even if the projection is going to stay as is though, users should be warned in the documentation about exactly what they’re getting.

gingery projections

Thank you this great plugin. I've had success changing the projection of my custom world topojson files. Particular enjoy the interrupted projections. But I couldn't manage to run the 'gingery' projection. Not sure the projection file has been updated with gingery details?

http://d3js.org/d3.geo.projection.v0.min.js

I've tried various versions of the code provide in the example http://www.jasondavies.com/maps/gingery/

e.g. var projection = d3.geo.gingery()

But without luck. I'll send a complete example of my code if you require.

Thank you

Decide of the good projection

Hi,

Please face to a map, which factors should we study in order to choose a projection function ?

Thanks.

Add bower support

path.fit(feature, extent)

It’d be nice to have a standard API for project to bounding box:

projection
    .scale(1)
    .translate([0, 0]);

var b = path.bounds(feature),
    s = tolerance / Math.max((b[1][0] - b[0][0]) / width, (b[1][1] - b[0][1]) / height),
    t = [(width - s * (b[1][0] + b[0][0])) / 2, (height - s * (b[1][1] + b[0][1])) / 2];

projection
    .scale(s)
    .translate(t);

One tricky thing is that you may need to increase the projection precision temporarily to compute the bounds (since the precision is scale-dependent, and the scale is being set to 1). Perhaps it’d be sufficient to re-scale the precision based on the prior values, and then restore them?

Tests for stitching.

From the TopoJSON 1.x tests:

//
// A-----B-----C-----D-----E
// |                       |
// |                       |
// J-----I-----H-----G-----F
tape("topology a polygon surrounding the South pole with a cut along the antimeridian", function(test) {
  var topology = topojson.topology({
    polygon: {type: "Polygon", coordinates: [[
      [-180, -80], [-90, -80], [0, -80], [90, -80], [180, -80],
      [180, -90], [90, -90], [0, -90], [-90, -90], [-180, -90],
      [-180, -80]
    ]]}}, 4);
  test.deepEqual(topology.arcs, [
    [[0, 3], [1, 0], [1, 0], [-2, 0]]
  ]);
  test.deepEqual(topology.objects.polygon, {type: "Polygon", arcs: [[0]]});
  test.end();
});

//
// B-----C-----D-----E-----F
// |                       |
// |                       |
// A                       G
// |                       |
// |                       |
// L-----K-----J-----I-----H
tape("topology a large polygon surrounding the South pole with a cut along the antimeridian", function(test) {
  var topology = topojson.topology({
    polygon: {type: "Polygon", coordinates: [[
      [-180, -85], [-180, -80], [-90, -80], [0, -80], [90, -80], [180, -80],
      [180, -85], [180, -90], [90, -90], [0, -90], [-90, -90], [-180, -90],
      [-180, -85]
    ]]}}, 5);
  test.deepEqual(topology.arcs, [
    [[0, 4], [1, 0], [1, 0], [1, 0], [-3, 0]]
  ]);
  test.deepEqual(topology.objects.polygon, {type: "Polygon", arcs: [[0]]});
  test.end();
});

//
// A-----B-----C-----D
// |                 |
// N                 E
//  \               /
//   M             F
//  /               \
// L                 G
// |                 |
// K-----J-----I-----H
tape("topology a large polygon with a hole across the antimeridian and cut along the antimeridian", function(test) {
  var topology = topojson.topology({
    polygon: {type: "Polygon", coordinates: [[
      [-180, -60], [-180, -30], [-150, 0], [-180, 30], [-180, 60], [-60, 60], [60, 60],
      [180, 60], [180, 30], [150, 0], [180, -30], [180, -60], [60, -60], [-60, -60], [-180, -60]
    ]]}}, 8);
  test.deepEqual(topology.arcs, [
    [[0, 7], [2, 0], [3, 0], [-5, 0]],
    [[0, 0], [5, 0], [-3, 0], [-2, 0]],
    [[0, 5], [6, -1], [-6, -2], [1, 2], [-1, 1]]
  ]);
  test.deepEqual(topology.objects.polygon, {type: "Polygon", arcs: [[0], [1], [2]]});
  test.end();
});

what am I doing wrong here?

would like to use d3.geo.centroid but...
node -e "var d3 = require('d3'); console.log(Object.keys(d3))"
doesn't contain "geo".
node -e "var d3 = require('d3'); require('d3-geo-projection')(d3);"
TypeError: Cannot set property 'project' of undefined.
node -e "var d3 = require('d3'); d3['geo'] = require('d3-geo-projection'); console.log(typeof d3.geo );"
function

.... any ideas?

Authagraph projection?

Been using D3 for a while and came across this:

http://www.spoon-tamago.com/2016/10/28/hajime-narukawa-authagraph/

Less an issue, more of a wow check out this projection in case someone is interested in implementing it. I'm not even remotely enough of a mapping person to even know where to start implementing this, but it seems like it would be a pretty valuable type of projection for a lot of people (me included).

Tobler hyperelliptical projection?

https://en.wikipedia.org/wiki/Tobler_hyperelliptical_projection

Error when using d3-geo-projection with d3 4.1?

I'm trying to use d3-geo-projection from within a Node.js context (to render some OSM data). I followed the instructions in the readme:

npm install d3 d3-geo-projection

and in my javascript:

var Canvas = require("canvas"),
    d3 = require("d3"),
    topojson = require("topojson"),
    rw = require("rw"),
    world = require("./world-110m.json");
require("d3-geo-projection")(d3);

But when I try to run this, I get:

undefined:4
  d3.geo.project = function(object, projection) {
                 ^

TypeError: Cannot set property 'project' of undefined
    at eval (eval at <anonymous> (/Users/iandees/Downloads/d32video/node_modules/d3-geo-projection/index.js:4:18), <anonymous>:4:18)
    at eval (eval at <anonymous> (/Users/iandees/Downloads/d32video/node_modules/d3-geo-projection/index.js:4:18), <anonymous>:1916:3)
    at Object.<anonymous> (/Users/iandees/Downloads/d32video/draw.js:9:29)
    at Module._compile (module.js:413:34)
    at Object.Module._extensions..js (module.js:422:10)
    at Module.load (module.js:357:32)
    at Function.Module._load (module.js:314:12)
    at Function.Module.runMain (module.js:447:10)
    at startup (node.js:146:18)
    at node.js:404:3

Myriahedral projections?

Given I have seen issues with requests for "fancy" map projections, why not proposing the fanciest?

Myriahedral map projections by Prof. Jarke van Wijk

thumbnails in README.md not visible

Visiting https://github.com/d3/d3-geo-projection does not show the thumbnails specified via raw.github.com

Cahill–Keyes projection?

I've dreamt for years now of porting the Cahill-Keyes butterfly projection to a GIS platform. The existing CK formulas are brute force, I'm sure there's a lot of room to simplify and convert to actual algorithms, but my math skills are too weak for the task (and my time management weaker!).

So I'm lobbing the ball over here in the hopes someone else will be sufficiently inspired to carry it out.

geo2svg --fill and --stroke

If you can pass a JavaScript expression to --fill and --stroke, you should have all the pieces needed to render a choropleth from data into a static SVG, which would be grand. (You can use ndjson-join to join the GeoJSON stream with a TSV stream of properties.)

The tricky part might be how to load d3 into one of these expressions, and how to define scales: mbostock/ndjson-cli#8.

Update to D3 4.0.

mercator projection missing

The readme suggests that there is a mercator projection as geoMercator, but it's not in the library.

Built-in interrupted projections.

Seems a bit strange that we don’t provide some of the standard interrupted projections as built-ins. For example, the interrupted Goode homolosine projection could be defined as:

import {homolosineRaw} from "./homolosine";
import interrupt from "./interrupt";

export default interrupt(homolosineRaw)
    .lobes([[ // northern hemisphere
      [[-180,   0], [-100,  90], [ -40,   0]],
      [[ -40,   0], [  30,  90], [ 180,   0]]
    ], [ // southern hemisphere
      [[-180,   0], [-160, -90], [-100,   0]],
      [[-100,   0], [ -60, -90], [ -20,   0]],
      [[ -20,   0], [  20, -90], [  80,   0]],
      [[  80,   0], [ 140, -90], [ 180,   0]]
    ]]);

fs.readFileSync is not a function

I am trying the node approach (using webpack):
var d3 = require("d3");
require("d3-geo-projection")(d3);

But I get this error:
Uncaught TypeError: fs.readFileSync is not a function

Any ideas?

Guyou and Pierce Quincuncial projections broken in Chrome 33

Haven’t investigated yet, but I assume it’s a numerical instability related to some change in Chrome’s trigonometric functions.

/cc @jasondavies

geoproject --require

We should support --require so that you can load third-party plugins such as d3-stateplane / d3-geo-state-plane.

Icosahedral map

I would like to create a gnomonic icosahedral map (not a Fuller map, just a simple icosaheral map based on a simple icosahedral net) but as a neophyte in this area, i take inspiration from the gnomonic buterfly (octahedron) and my difficulty is to understand these lines in the buterfly.js code:

[-1, 0, 0, 1, 0, 1, 4, 5].forEach(function(d, i) {
    var node = faces[d];
    node && (node.children || (node.children = [])).push(faces[i]);
 });

What is the array [-1, 0, 0, 1, 0, 1, 4, 5] ? Could you give some reference to understand that ?
Thanks.

SyntaxError: Invalid character '\u8224'

I am using d3 and d3.geo.projections to render a map of some simplified admin0 data. I am also using codekiy with uglify to compile my code. All goes well until I append d3.geo.projections.js.

There after my map does not render and I get an error message of in my console:
SyntaxError: Invalid character '\u8224'
...which seems to refer to some special characters in country names. For example "Saint Barthï¿½lemy"

However, I am not using any of the extended projections yet, I get the error just from including the script. Uninclude the extended projections and the error goes away. Can you offer any thoughts?

geo2svg

As part of #72.

Group README by projection properties.

Inspired partly by https://en.wikipedia.org/wiki/List_of_map_projections, some possible categories:

conformal
equal-area
equidistant
retroazimuthal
compromise
other
interrupted (and polyhedral?)

Wrong naming with deployed via bower

In the "bower_components/d3-geo-projection" folder, the file name is:

d3.geo.projection.js

In the bower.json file, it has the "name" and "main" as "d3-geo-projection" and "d3-geo-projection.js".

In my Angular project, I'm using wiredeps and it's automatically including the "d3-geo-projection.js" file which can't be found since the file is using periods instead of dashes.

So the solution is to rename the file to use dashes or fix the bower.json config to use periods.

geoStitch and geoQuantize should NOT modify in-place.

This was a lazy decision since they were only used on the command-line, but now that they are accessible programmatically, we should have them return copies. (And bump the major version number of this module to be safe.)

d3.geoProject is not a function

Main problem

d3.geoProject is not recognized as a function, so I can't use it in my script.

Why I need to use it in script and not in command line ?

Because, my geojson file is big (~100Mo) and with geoproject 'd3.geoConicEqualArea()' < file1.json > file2.json it fires FATAL ERROR: CALL_AND_RETRY_LAST Allocation failed - JavaScript heap out of memory.

Solution and main problem

So the solution was to run node with more memory, with the flags --max_old_space_size=16384 --optimize_for_size --max_executable_size=16384 --stack_size=16384 to allow 16Go of memory. Unfortunately, I can't run global package with these flags. So I need to wrap it up in a script and run it from my package.json.

Then I came with the problem that d3.geoProject is not a function. But I thought it was because of: https://github.com/d3/d3-geo-projection#geoProject and https://github.com/d3/d3-geo-projection/blob/master/bin/geoproject#L40

Infos

node v7.5.0
npm v4.2.0
d3 ^4.5.0

Thanks for your help

Berghaus projection is a bit broken.

http://bl.ocks.org/mbostock/4463049

Supersedes d3/d3-plugins#57 and d3/d3#1158.

Expose d3.geoQuincuncial?

Antimeridian Cutting for interrupted projections

The antimeridian cutting is such a great feature!
However, it seems it cannot work for interrupted projections.

I modified the code of Antimeridian Cutting example to change to projection to "geoInterruptedHomolosine" and it cannot cut properly.

Error started appearing after recent release to 4.7.1

Greetings!

We have some geoJSON files that are giving us unexpected errors after the recent release of 4.7.1. Not all of them are failing, which is strange. All of the ones that are failing validate in a geoJSON validator just fine. No changes have been made to these files in the last 4 months.

The error we receive is "Error: attribute d: Expected number, "MNaN,NaNLNaN,NaN"
Our code is below. And the JSON is attached.
0157_02_json.txt

Any idea why this is happening?
`
vm.projection = d3.geoMercator().rotate([0, vm.rotation]);
vm.path = d3.geoPath()
.projection(vm.projection.fitExtent([[0, 0], [vm.w, vm.h]], json));

            vm.svg.selectAll(".room")
                .data(vm.rooms)
                .enter().append("path")
                .attr("class", "room")
                .attr("d", vm.path)
                .attr("fill", "#fff")
                .attr("stroke", "none")
                .attr("id", function (d) {
                    return d.properties.loc;
                })
                .on("mouseover", function (d) {
                    vm.div.transition()
                        .duration(90)
                        .style("opacity", 1);
                    vm.div.html(d.properties.room)
                        .style("left", (d3.event.pageX) + "px")
                        .style("top", (d3.event.pageY - 28) + "px");
                })
                .on("mouseout", function (d) {
                    vm.div.transition()
                        .duration(90)
                        .style("opacity", 0);
                })
                .on('click', function (d) {
                    d3.selectAll(".room").attr("fill", "#fff").attr("stroke", "none");
                    d3.select(this).attr("fill", "#BBDEFB").attr("stroke-width", "2").attr("stroke", "#FF5722");
                    vm.handleClick(d);
                });`

Error: "toString()" failed

I have a .shp file of the whole globe. I tried using geostitch since I have a full globe and I get a similar error. Not sure if I am missing a js dependency or something else.

shp2json ~/data/mapping/world-combo-new/betas.shp -o world.json #this works

geoproject 'd3.geo.cylindricalEqualArea().parallel(37.5).fitSize([960,960],d)' < world.json > world-mercator.json


Error: "toString()" failed
    at Buffer.toString (buffer.js:495:11)
    at Object.parse (native)
    at ReadStream.<anonymous> (/usr/local/lib/node_modules/d3-geo-projection/bin/read.js:13:48)
    at emitNone (events.js:91:20)
    at ReadStream.emit (events.js:185:7)
    at endReadableNT (_stream_readable.js:974:12)
    at _combinedTickCallback (internal/process/next_tick.js:74:11)
    at process._tickCallback (internal/process/next_tick.js:98:9)```

Recommend Projects

React

A declarative, efficient, and flexible JavaScript library for building user interfaces.
Vue.js

🖖 Vue.js is a progressive, incrementally-adoptable JavaScript framework for building UI on the web.
Typescript

TypeScript is a superset of JavaScript that compiles to clean JavaScript output.
TensorFlow

An Open Source Machine Learning Framework for Everyone
Django

The Web framework for perfectionists with deadlines.
Laravel

A PHP framework for web artisans
D3

Bring data to life with SVG, Canvas and HTML. 📊📈🎉

Recommend Topics

javascript

JavaScript (JS) is a lightweight interpreted programming language with first-class functions.
web

Some thing interesting about web. New door for the world.
server

A server is a program made to process requests and deliver data to clients.
Machine learning

Machine learning is a way of modeling and interpreting data that allows a piece of software to respond intelligently.
Visualization

Some thing interesting about visualization, use data art
Game

Some thing interesting about game, make everyone happy.

Recommend Org

Facebook

We are working to build community through open source technology. NB: members must have two-factor auth.
Microsoft

Open source projects and samples from Microsoft.
Google

Google ❤️ Open Source for everyone.
Alibaba

Alibaba Open Source for everyone
D3

Data-Driven Documents codes.
Tencent

China tencent open source team.