d3 / d3-geo-polygon Goto Github PK

View Code? Open in Web Editor NEW

107.0 14.0 22.0 10.98 MB

Clipping and geometric operations for spherical polygons.

Home Page: https://observablehq.com/collection/@d3/d3-geo-polygon

License: Other

JavaScript 100.00%

d3-geo-polygon's Introduction

d3-geo-polygon

Clipping and geometric operations for spherical polygons.

Installing

If you use npm, npm install d3-geo-polygon. You can also download the latest release on GitHub. For vanilla HTML in modern browsers, import d3-geo-polygon from Skypack:

<script type="module">
import {geoCubic} from "https://cdn.skypack.dev/d3-geo-polygon@2";
const projection = geoCubic();
</script>

For legacy environments, you can load d3-geo-projection’s UMD bundle from an npm-based CDN such as jsDelivr; a d3 global is exported:

<script src="https://cdn.jsdelivr.net/npm/d3-array@3"></script>
<script src="https://cdn.jsdelivr.net/npm/d3-geo@3"></script>
<script src="https://cdn.jsdelivr.net/npm/d3-geo-polygon@2"></script>
<script>

const projection = d3.geoCubic();

</script>

This module introduces a handful of additional projections. It can also be used to clip a projection with an arbitrary polygon:

const projection = d3.geoEquirectangular()
  .preclip(d3.geoClipPolygon({
    type: "Polygon",
    coordinates: [[[-10, -10], [-10, 10], [10, 10], [10, -10], [-10, -10]]]
  }));

API Reference

# d3.geoClipPolygon(polygon) · Source, Examples

Given a GeoJSON polygon or multipolygon, returns a clip function suitable for projection.preclip.

# clip.polygon([geometry])

If geometry is specified, sets the clipping polygon to the geometry and returns a new clip function. Otherwise returns the clipping polygon.

# clip.clipPoint([clipPoint])

Whether the projection should clip points. If clipPoint is false, the clip function only clips line and polygon geometries. If clipPoint is true, points outside the clipping polygon are not projected. Typically set to false when the projection covers the whole sphere, to make sure that all points —even those on the edge of the clipping polygon— get projected.

# d3.geoIntersectArc(arcs) · Source, Examples

Given two spherical arcs [point0, point1] and [point2, point3], returns their intersection, or undefined if there is none. See “Spherical Intersection”.

Projections

d3-geo-polygon adds polygon clipping to the polyhedral and interrupted projections from d3-geo-projection. Thus, it supersedes the following symbols:

# d3.geoPolyhedral(tree, face) · Source, Examples

Defines a new polyhedral projection. The tree is a spanning tree of polygon face nodes; each node is assigned a node.transform matrix. The face function returns the appropriate node for a given lambda and phi in radians.

Polyhedral projections’ default clipPoint depends on whether the clipping polygon covers the whole sphere. When the polygon’s area is almost complete (larger than 4π minus .1 steradian), clipPoint is set to false, and all point geometries are displayed, even if they (technically) fall outside the clipping polygon. For smaller polygons, clipPoint defaults to true, thus hiding points outside the clipping region.

# polyhedral.tree() returns the spanning tree of the polyhedron, from which one can infer the faces’ centers, polygons, shared edges etc.

# d3.geoPolyhedralButterfly() · Source

The gnomonic butterfly projection.

# d3.geoPolyhedralCollignon() · Source

The Collignon butterfly projection.

# d3.geoPolyhedralWaterman() · Source

A butterfly projection inspired by Steve Waterman’s design.

# d3.geoBerghaus · Source

The Berghaus projection.

# d3.geoGingery · Source

The Gingery projection.

# d3.geoHealpix · Source

The HEALPix projection.

# d3.geoInterruptedBoggs · Source

Bogg’s interrupted eumorphic projection.

# d3.geoInterruptedHomolosine · Source

Goode’s interrupted homolosine projection.

# d3.geoInterruptedMollweide · Source

Goode’s interrupted Mollweide projection.

# d3.geoInterruptedMollweideHemispheres · Source

The Mollweide projection interrupted into two (equal-area) hemispheres.

# d3.geoInterruptedSinuMollweide · Source

Alan K. Philbrick’s interrupted sinu-Mollweide projection.

# d3.geoInterruptedSinusoidal · Source

An interrupted sinusoidal projection with asymmetrical lobe boundaries.

# d3.geoTwoPointEquidistant(point0, point1) · Source

The two-point equidistant projection, displaying 99.9996% of the sphere thanks to polygon clipping.

# d3.geoTwoPointEquidistantUsa() · Source

The two-point equidistant projection with points [-158°, 21.5°] and [-77°, 39°], approximately representing Honolulu, HI and Washington, D.C.

New projections

New projections are introduced:

# d3.geoPolyhedralVoronoi([parents], [polygons], [faceProjection], [faceFind]) · Source

Returns a polyhedral projection based on the polygons, arranged in a tree.

The tree is specified by passing parents, an array of indices indicating the parent of each face. The root of the tree is the first face without a parent (with the array typically specifying -1).

polygons are a GeoJSON FeatureCollection of geoVoronoi cells, which should indicate the corresponding sites (see d3-geo-voronoi). An optional faceProjection is passed to d3.geoPolyhedral() -- note that the gnomonic projection on the polygons’ sites is the only faceProjection that works in the general case.

The .parents([parents]), .polygons([polygons]), .faceProjection([faceProjection]) set and read the corresponding options. Use .faceFind(voronoi.find) for faster results.

# d3.geoCubic() · Source, Examples

The cubic projection.

# d3.geoDodecahedral() · Source, Examples

The pentagonal dodecahedral projection.

# d3.geoRhombic() · Source, Examples

The rhombic dodecahedral projection.

# d3.geoDeltoidal() · Source, Examples

The deltoidal hexecontahedral projection.

# d3.geoIcosahedral() · Source, Examples

The icosahedral projection.

# d3.geoAirocean() · Source, Examples

Buckminster Fuller’s Airocean projection (also known as “Dymaxion”), based on a very specific arrangement of the icosahedron which allows continuous continent shapes. Fuller’s triangle transformation, as formulated by Robert W. Gray (and implemented by Philippe Rivière), makes the projection almost equal-area.

# d3.geoCahillKeyes() · Source, Examples
# d3.geoCahillKeyes

The Cahill-Keyes projection, designed by Gene Keyes (1975), is built on Bernard J. S. Cahill’s 1909 octant design. Implementation by Mary Jo Graça (2011), ported to D3 by Enrico Spinielli (2013).

# d3.geoImago() · Source, Examples

The Imago projection, engineered by Justin Kunimune (2017), is inspired by Hajime Narukawa’s AuthaGraph design (1999).

# imago.k([k])

Exponent. Useful values include 0.59 (default, minimizes angular distortion of the continents), 0.68 (gives the closest approximation of the AuthaGraph) and 0.72 (prevents kinks in the graticule).

# imago.shift([shift])

Horizontal shift. Defaults to 1.16.

# d3.geoTetrahedralLee() · Source, Examples
# d3.geoLeeRaw

Lee’s tetrahedral conformal projection.

# Default angle is +30°, apex up (-30° for base up, apex down).

Default aspect uses projection.rotate([30, 180]) and has the North Pole at the triangle’s center -- use projection.rotate([-30, 0]) for the South aspect.

# d3.geoCox() · Source, Examples
# d3.geoCoxRaw

The Cox conformal projection.

# d3.geoComplexLog([planarProjectionRaw[, cutoffLatitude]]) · Source, Example
# d3.geoComplexLogRaw([planarProjectionRaw])

Complex logarithmic view. This projection is based on the papers by Joachim Böttger et al.:

The specified raw projection planarProjectionRaw is used to project onto the complex plane on which the complex logarithm is applied. Recommended are azimuthal equal-area (default) or azimuthal equidistant.

cutoffLatitude is the latitude relative to the projection center at which to cutoff/clip the projection, lower values result in more detail around the projection center. Value must be < 0 because complex log projects the origin to infinity.

# complexLog.planarProjectionRaw([projectionRaw])

If projectionRaw is specified, sets the planar raw projection. See above. If projectionRaw is not specified, returns the current planar raw projection.

# complexLog.cutoffLatitude([latitude])

If latitude is specified, sets the cutoff latitude. See above. If latitude is not specified, returns the current cutoff latitude.

d3-geo-polygon's People

Contributors

Stargazers

Watchers

d3-geo-polygon's Issues

polygon clipping errors

while these first two could be solved by clipping to the sphere, the last one shows we still sometimes have inversions:

(reported by @mootari @ https://imgur.com/a/Km2wK6m)

Easier usage with d3.geoProject?

It’d be nice if this library were easier to use when saving spherically-clipped GeoJSON. For example:

https://beta.observablehq.com/d/d706c7f9c6e46907

The tedious parts are:

You need to wrap the d3.geoClipPolygon instance with an object that has a stream method.
You need to compose the d3.geoClipPolygon instance with streams that transform from degrees to radians and then back again.

Part of me wonders if it’s worth revisiting a more composable geographic projection pipeline…

(Also, I think d3.geoProject sometimes breaks polygon semantics, but that’s a separate issue.)

Examples using d3-geo-polygon

http://blockbuilder.org/Fil/90c1d39fa1b92281fd119c02188da858 shows how to use this plugin. It calls a modified version of d3.polyhedral (in d3-geo-projection) that in turn uses d3.geoClipPolygon(). More soon on this.

Older examples are available from https://bl.ocks.org/Fil/fc967d8ac6aa246863c6f2a4b7dbe41c and will be updated progressively.

Examples should go in the README when they're ready.

Markley

https://observablehq.com/@fil/markley

Tetrahedral Lee: Inverse broken?

Hello,

the inverse of the Tetrahedral Lee does not seem to work.
I’ve used the script by @cambecc – see here – to try this. Here is a demo, on top is the Imago projection where the inverse works (everything’s filled with blue pixels) but on the Lee, I only get a red triangle.

Am I doing something wrong or is the inverse broken?

Kind regards,
Tobias

cut not clip

Can we use this to cut (instead of clipping) to the polygon.

Would be useful to avoid disappearing points that are just on the edge of the polygon in polyhedral projections.
See d3/d3-geo-projection#132 (comment)

is it possible to only draw some of the faces?

i can only draw the first face by setting .parents([-1])

but if i only wanted to draw for example the first 3 faces of a cube would that be possible?

i have this question as i like to laser cut the faces out of would an turn them into a globe.
Drawing only a few faces would make it easier to fit on the laser cutter.

Failure with points that are exactly on the clipping polygon

The equator is broken (missing some parts, and bleeding out in other parts) at
http://blockbuilder.org/Fil/ee9bf16bf8b2fa56057733c443832c5d

clipping bug

In https://observablehq.com/@fil/oronce-fines-triangle-projection the graticule was properly clipped until [email protected], but it failed with release 1.8.0.
I think the offending commit is eb1e663 (#160).

Test @ https://observablehq.com/@fil/clipping-bug-39

This is also the reason why #60 (rhombic) had a small rotation. Same bug appears in https://observablehq.com/d/8085f693f9972f0e (#9)

[Cahill-Keyes] Re-assemble and attach Antarctica

https://beta.observablehq.com/@fil/cahill-keyes-projection#Antarctica

planar polygon clipping

The Imago projection needs to use polygon clipping; but it seems a bit absurd that we are doing spherical clipping (with 200 control points computed as the inverse of 200 planar points) just to do what is in the end a simple rectangular clipping. The thing is tricky because, so close to the limit, the spherical interpolation between control points might jump from one side to the other.

use robust-predicates?

https://github.com/mourner/robust-predicates

faster Voronoi projection

see https://beta.observablehq.com/@fil/speed-of-the-voronoi-projection

The projection is 100x faster if it can use geovoronoi.find() to know to which face a point belongs. In my local branch, I've solved this by allowing to pass a faceFind function.

But should we limit ourselves to this, or be bolder and pass a full geoVoronoi object (which would also help in finding shared edges much faster, by using the delaunay topology)?

[Cahill-Keyes] Inverse projection

https://beta.observablehq.com/@fil/cahill-keyes-projection

Can this library be used with other projections?

Namely, d3.geoAlbers? I am trying to use preclipping and am getting very strange results.

More to the point.
Polygon 1:
[ [ [ 30, 60 ], [ 90, 60 ], [ 90, 30 ], [ 30, 30 ], [ 30, 60 ] ] ]
Polygon 2:
[ [ [ 45, 75 ], [ 75, 75 ], [ 75, 15 ], [ 45, 15 ], [ 45, 75 ] ] ]

Projection:
d3.geoAlbers() .rotate([-105, 0]) .center([-10, 65]) .parallels([52, 64]);

Below is a picture made in qGis, cyan polygon (P2) is being clipped, green is the one doing the clipping (P1) (the one passed to geoClipPolygon and the result passed to preclip). Both polygons are already projected (but not preclipped).

After projecting, P2 is null.

Tried adding parents to TetrahedralLee

Hi,

i made some changes to TetrahedralLee so i can add parents and it also supports setting the root of the tree in other places than faces[0]. I added it to my fork here if you want to see.

Here are some images created whith the snapshot unittests

i also tried generating svg's but that is not working flawless yet.

d3.geoVoronoi() is not (yet) existing?

First, thanks for your great contributions regarding projections in D3. I have been playing with your new added projections in this d3-geo-polygon extension in combination with vega. Firstly I used the airocean projection to cut and engrave some wood using laser and liked the result¹.

But now having seen these maps on https://beta.observablehq.com/@fil/speed-of-the-voronoi-projection I would love to play with this projection as well.

I used the method as mentioned in the notebook:

The following map was made with the Voronoi projection — available as d3.geoVoronoi() in d3-geo-polygon.

When I try to use this:
projection = d3.geoVoronoi()

I receive:
TypeError: d3.geoVoronoi is not a function

Question: I'm trying features that are not yet available? or do I call them wrongly?

¹ Click to expand

Inverse clipping on d3.geoClipPolygon

Sorry noob question here...how do i inverse the clipping of d3.geoClipPolygon with preclip?...any example would be appreciate

South aspect of Lee’s conformal projection in a tetrahedron is all black

South aspect of Lee’s conformal projection in a tetrahedron shows all black.

From the tweet exchange @Fil has verified that

it doesn't happen with [email protected] but with [email protected]

Clean up Waterman / Cahill

The issue is described here: d3/d3-geo-projection#125

To sum up this would need to:

introduce geoCahill1909 (which would be geoPolyhedralWaterman but with the inferior choice of angles from Cahill's original — and that could be a parameter of course), and be mindful of the face projection used in 1909
create a "true" geoWaterman with Antarctica cut out (see also #11)
obsolete geoPolyhedralWaterman

Node >10.17.0 support

This package is constrained to node ">=6.0.0 <=10.17.0". Using this package with maintained node versions without ignoring engines constraint isn't possible. Is there any reason why this constraint is present in d3-geo-polygon package.json?

Part of API doesn't seem to rely on node internals eg. geoArcIntersect. Maybe if part of API needs old node version it'll be good idea to move independent code parts into other package.

deltoidal hexecontahedron projection

Hi,

i created a deltoidal hexecontahedron projection which can be seen here.

https://observablehq.com/d/881a8431e638b408

would this be a welcome addition to the project? I based it on d3.geoPolyhedralVoronoi()

fix HEALPix?

https://github.com/d3/d3-geo-projection#geoHealpix could use a clipPolygon

named imports fail in webpack build.

Trying to bundle this in a webpack-based app, I find it breaks because it assumes a hardcoded location for node_modules in many places, eg (from here).

import {abs, degrees, epsilon, radians} from "../../node_modules/d3-geo-projection/src/math";
import {default as matrix, multiply, inverse} from "../../node_modules/d3-geo-projection/src/polyhedral/matrix";

yielding many errors like

ERROR in ./node_modules/d3-geo-polygon/src/polyhedral/waterman.js
Module not found: Error: Can't resolve '../../node_modules/d3-geo-projection/src/math' in '/home/bschmidt/project/node_modules/d3-geo-polygon/src/polyhedral'

Since I'm also requiring d3-geo-projection, these files are not inside the d3-geo-polygon folder: they're located at something like '../../../node_modules', maybe a level higher.

I'm able to get a successful install by just removing the prefix in all javascript files and importing straight from (eg) d3-geo-projection/src/math

~/project/node_modules/d3-geo-polygon/ find . -name "*.js" | xargs -I {} -n 1 perl -pi -e 's/\..\/\..\/node_modules\///g' {}

Can file a pull request if desired, but I don't know if that fix will break in other locations.

Thanks!

epsilon3 and intersect(a, b)

From Jason Davies's code (ported in 82d9481#diff-1955ba130f17ffd3f1a5db97ee798e02R13 ), there was an epsilon2 test in this function.

Somehow it allowed lines to escape the clipping on some occasions, so I lowered it to epsilon3 in 202e604 and got much less errors.

But it still happens, and the fix is to get rid of any epsilon and compare the values with 0.

I wonder what I'm missing (in which cases this value should be st. positive), but testing in all my examples seems to be OK with 0 instead of epsilon3.

rhombic dodecahedron test produces weird results probably something i am missing

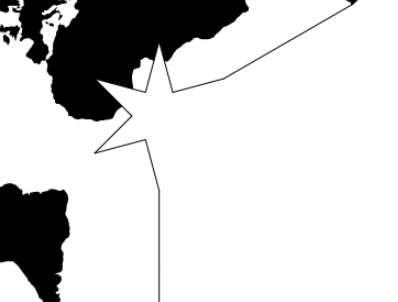
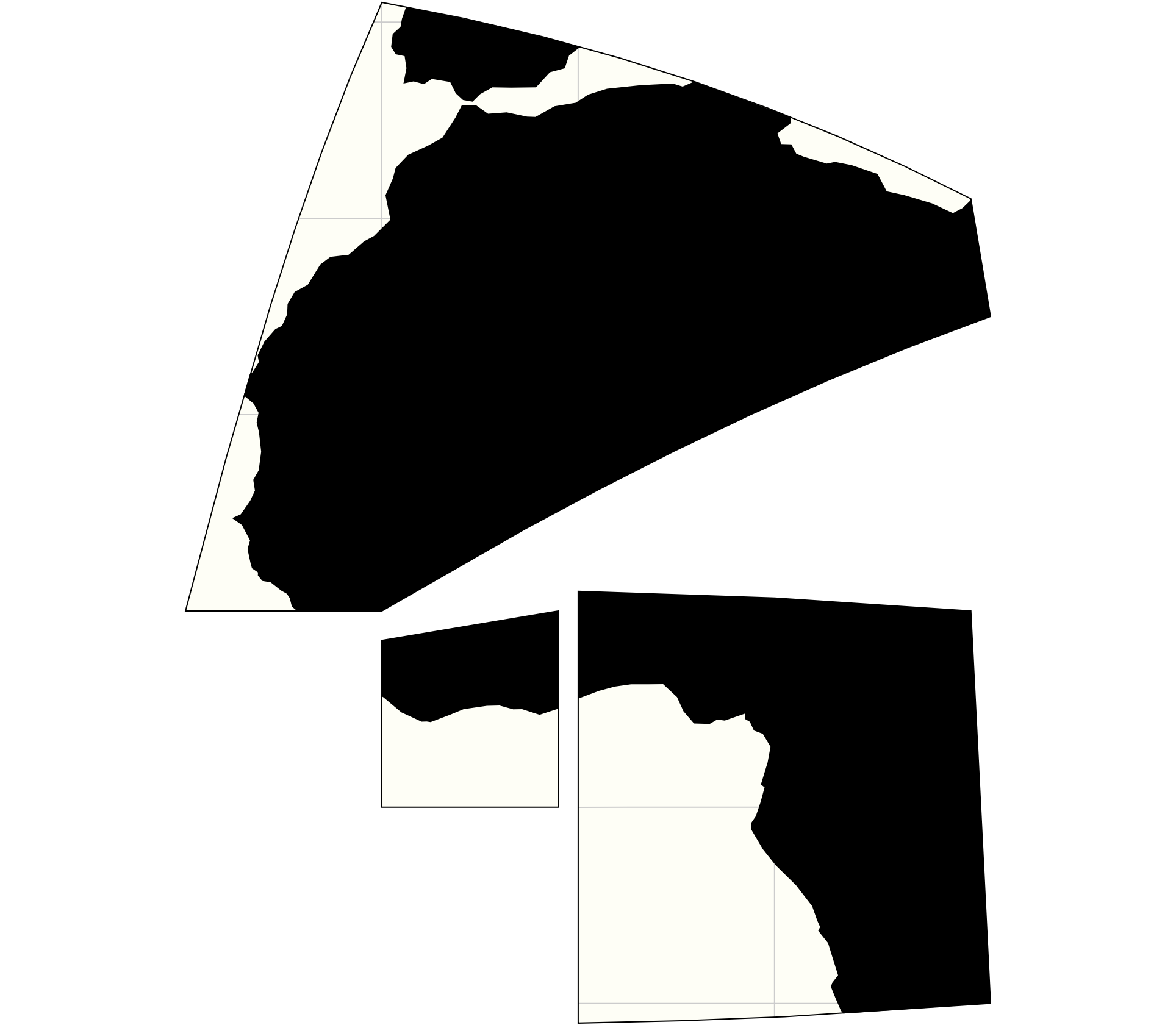
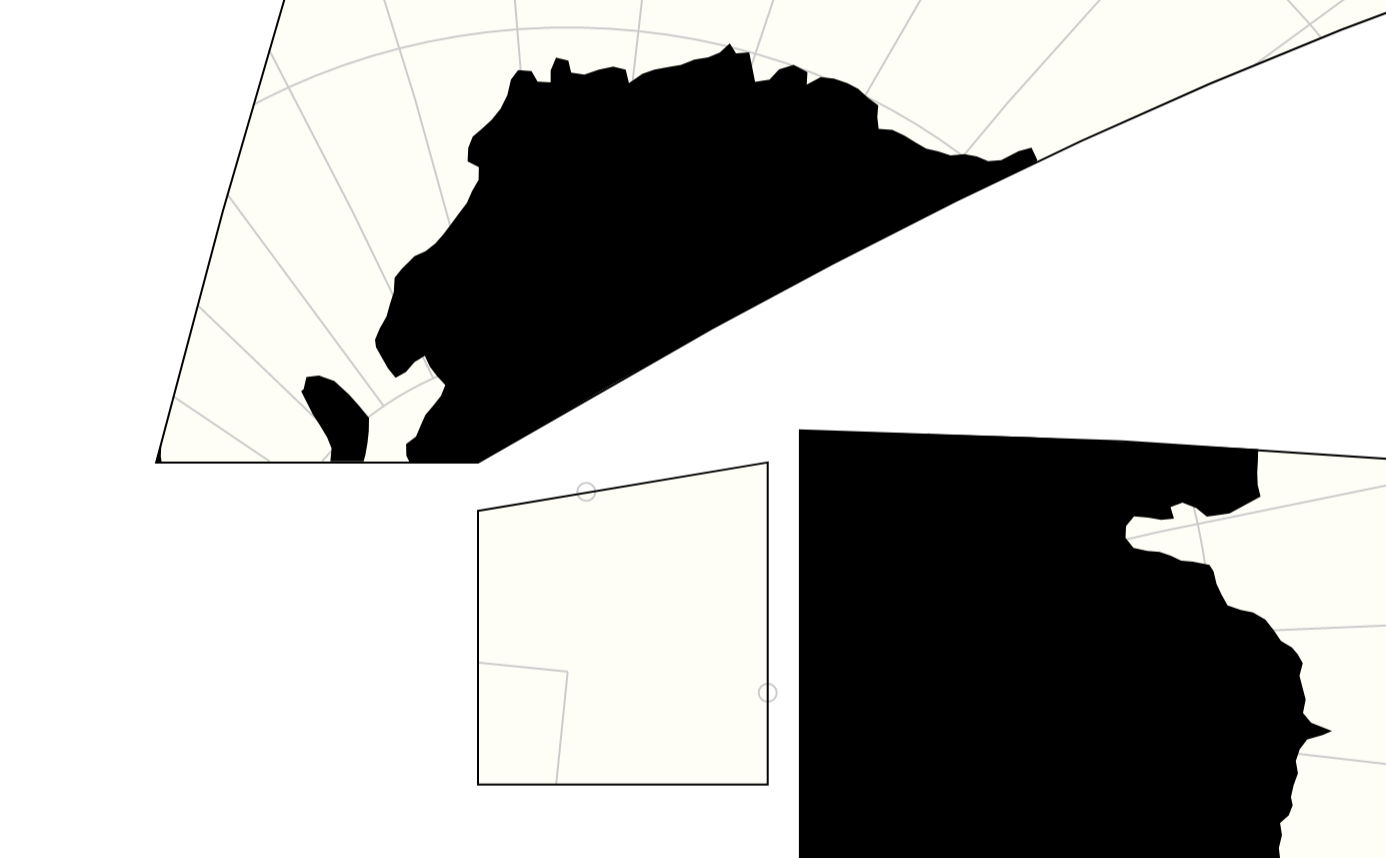
So i was trying to create a rhombic dodecahedron projection but there is something weird going on with the clipping

rhombic_f = {
  var degrees = 180 / Math.PI;
  var phi1 = Math.atan(Math.SQRT1_2) * degrees;
  var vertices = [
    [0, 90],      // 0
    [0, phi1],    // 1
    [90, phi1],   // 2
    [180, phi1],  // 3
    [-90, phi1],  // 4
    [45, 0],      // 5
    [135, 0],     // 6
    [-135, 0],     // 7
    [-45, 0],     // 8
    [0, -phi1],   // 9
    [90, -phi1],  // 10
    [180, -phi1], // 11
    [-90, -phi1], // 12
    [0, -90]      // 13
  ];
    
  // rhombic dodecahedron
  var polyhedron = [
    [0, 1, 8, 4],
    [0, 2, 5, 1],
    [0, 3, 6, 2],
    [0, 4, 7, 3],

    [1, 5, 9, 8],
    [2, 6, 10, 5],
    [3, 7, 11, 6],
    [4, 8, 12, 7],

    [8, 9, 13, 12],
    [5, 10, 13, 9],
    [6, 11, 13, 10],
    [7, 12, 13, 11]
  ].map(function(face) {
          return face.map(function(i) {
            return vertices[i];
          });
  });

  var polygons = {
    type: "FeatureCollection",
    features: polyhedron.map(function(face) {
      face.push(face[0]);
      return {
        properties: { sitecoordinates: d3.geoCentroid({type:"MultiPoint", coordinates: face}) },
        geometry: {
          type: "Polygon",
          coordinates: [ face ]
        }
      };
    })
  };

var parents = [
      -1, // 0
      0, // 1
      6, // 2
      2, // 3
      1, // 4
      9, // 5
      11, // 6
      3, // 7
      4, // 8
      8, // 9
      5, // 10
      10, // 11
    ];

  //return polygons;
  return d3.geoPolyhedralVoronoi()
   .parents(parents)
   .polygons(polygons);
};

i numbered the faces in the image below and there should be red lines around all the faces. This is a combination of the cubic and the octahedron projection.

[Cahill-Keyes] Conformal version

We could use the Schwarz-Christoffel transformation. http://www.genekeyes.com/CAHILL-VARIANTS/Cahill-Conformal.html shows one made by @jrus

Multiple broken links in examples

Hi, many of the links to examples on scratchpad don't work. In particular, I want the https://beta.observablehq.com/@fil/icosahedral-projection

Roşca-Plonka projection?

See https://beta.observablehq.com/@fil/an-equal-area-projection-for-the-cubic-earth

Is there any interest in integrating this equal-area square face projection? (It can be fun to use on something else than the 1/6th square face of the cube.) If so, should it be integrated in this module or in d3-geo-projection?

Use clipPolygon for geoInterrupted

example code that works (at least in one test case):

var c = projection.lobes().map(d => d3.merge(d.map(q => {
  var centroid = d3.geoCentroid({type:"MultiPoint", coordinates:q});
  return q.map(p => d3.geoInterpolate(p,centroid)(1e-7)); // pull inside each lobe
})));
c = d3.merge([c[0], c[1].reverse()]); // north, south
projection.preclip(d3.geoClipPolygon({ type: "Polygon", coordinates: [c] }));

the projection was defined by:

    var lobes = [
      [
        [[-180, 0], [-130, 90], [-95, 0]],
        [[-95, 0], [-30, 90], [55, 0]],
        [[55, 0], [120, 90], [180, 0]]
      ],
      [
        [[-180, 0], [-120, -90], [-60, 0]],
        [[-60, 0], [20, -90], [85, 0]],
        [[85, 0], [140, -90], [180, 0]]
      ]
    ];
    projection = d3.geoInterrupt(d3.geoHomolosineRaw, lobes).rotate([-204, 0])
    .fitExtent([[10, 10], [width-10, height-10]], {type: "Sphere"});

Clipping artefacts on rotate

I was playing around and got some clipping problem.
This code map(d3.geoCubic().parents([-1, 2, 0, 2, 5, 2]).rotate([0,0,45])) produces some artefacts:

map() as per https://beta.observablehq.com/@fil/polyhedral-projections-with-d3-geo-polygon

geoDesic

Hi,

I was messing around again and created a v2 geoDesic projection. I starts of with the icosahedron and splits up the triangle in sub triangles. For a v2 a triangle is split up into 4 sub triangles.

Here is an example

I am currently working on making the projection parametric so geoDesic(2) would create a v2 and geoDesic(3) would create a v3.

If you are interested in adding this I can create a pull request.

MultiPolygon clipping

The multipolygon branch is a first step towards #9 and #11.

There is a demo here:
https://beta.observablehq.com/d/368627e7d1bcc0cb

each polygon is processed in turn.

There are still a few bugs though — as you can see if you rotate the map in the demo, there are sometimes mix-ups in the variables that control the points' visibility, resulting in dots for points that should belong to a polygon, or in full-white surfaces that should be full-black.